Lösung von Zusatzaufgabe 10.2P (WS 12 13): Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
<ggb_applet width="1339" height="690" version="4.2" ggbBase64="UEsDBBQACAgIANxmNEIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADcZjRCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1c23LbNhq+Tp8Co4u9immcD127nTat7aRut7Pp7uzsTYaSaImxTGpF+tTp4+yb7IvtB4DUwZYc2bFdOk4cCCSOH/7TB0DZ+/bqbEIuslmVl8V+jyW0R7JiUA7zYrTfO69Pdmzv22++2htl5Sjrz1JyUs7O0nq/JxPeW9RDLmHcV86H+z1KM6szLXdsNtQ7klm3Y41Od6hx/fREpQPKdY+Qqyr/uih/Sc+yapoOsveDcXaWHpeDtA5tjut6+vXu7uXlZdL2npSz0e5o1E+uqmGPYORFtd9rPnyN5lYqXYpQnFPKdv/183FsficvqjotBlmP+Fmd59989WrvMi+G5SW5zIf1GBgIjdGNs3w0xjwNtz2y60tNMdlpNqjzi6xC3aVsmHR9Nu2FYmnh37+Kn8hkPp8eGeYX+TCbAaCEKWGEUNwqRRXjUvVIOcuzom4Ks6bT3ba5vYs8u4zt+k+hS0mdwSLkVd6fZPu9k3RSYV55cTIDphjR7BzZqr6eZP101uYXA2Kv8QcF8t8z3xYWLwKx3xNCvLbutaH0NcYXh7Lcb4/UZTkJjVKiHPnjD8Ipp+S1T1hMOBKt4ysan1EREx4TGRMVy8hYXcaiMpaRsYwUd0yzyW+ep1jMklO1mCXD9Pyvxm+Y/o1p2qVpMj+HPwjzgw+JIH7YLAzfJ7LJ6pg1IWE0Jqx5af0/AS59nwk1D5ZXTrQzYsvr9qkZsaVeI0rbozjHkAnhtu+Sf9bKLWa5Zt242jDLzwR33qlaghZ9hb/h91aX4rOm+ZAetfwczX9Ah4auaH2r8jFlTXoXDI82qL3d1hbuNQMi1diXbUS6zs4qP0Thgm0ijCgorzYwJYowh8R4JeaEKSIVsswS7VNDhNdbSQSxxJdjggQLpCz+kUGnNVFoyz80UbmJkEQJwoLdkgQokGD7gAkXKKEUUajke2e+W6GJ1MgISyQG6K2e8aZFoB7y6JwTwYjwdZkhXBPNifGWk0lvULX1Y0ejnGhKtK8K0wmzGU0malgi/GygBdOyyufgjrPJdL4qAce8mJ7XK9gNzobtx7q8UXpYDk6/v4F1llZ1+xmF4K4WXjG6rxWn+WpvkvazCWKL914MCLlIJ17LQ/snZVGTVgR4fDaapdNxPqjeZ3WNWhX5mF6kx2mdXR2gdNUOMHQdnPledj6Y5MM8Lf4JGfFN+AbJwrd729X6dqWbrgdlORu+v64gOeTq39mshH4Jmrjlnx65jm+4UAlf/vFWapB6ked89Q2Dkl5veEdl7Du7mE8uvcqqFs3RzCtdg7/PvK2+LyeLR9MyL+o36bQ+n4VQDYOY+Vl9V4wmWUA32F4EPYPTfnn1vjHdsa3frqfI0TiA/uhNOSlnBCrJFczsqEn7MQ1l/MjmpWgoQ0MJ2q5TPpy/Z46HEiHtxzSUwsLHoTUzZe00GW27yasYQfZWxCxIjY+gzou8Pm4zdT44bWbKYvlfzs/6ELim2mqT7JGa3Nu9IWJ7p9msyCZRjgqs5Hl5XkXJnkvnq73zKvs1rcffFcO/ZyOo5K+pt4o1mo5FFyMeZoP8DBXj8wa61C/rPzDU+HSYjWZZO8NJiI0jsOEtXZbqW49DUwez8uxtcfEbZObGUPd22/nsVYNZPvWiSfow06fZQvqGeZXCyA+X62HyFWYx8AYHQNYexB5Jz+txOQvRL9TWR2Dk3f/+WxTZDJYS8uhVdpKdIfIldZDKINjz9fkuxNR+IUjZ/whDcmP9FrDh9VoJDbKcTqbj1MfdDQaT9BoDWEYltPdzObyJFZYiTAi2YRqFYpplUZziePFhiuaCEi6tdwC/Ilf7vR2dGCjCtWdJDkb590izIqfwk/W6uWIJ49MbCwe5izh9ArHvvwDEeGJ1QGyHJYo/CmSD8uwsLYakCLHIMSxRb+ECU+oljaTMwxexOa/bF2lsqmngFvreqM3BTT8B/tJ0N6FPH479AkGdSBsAFAFJ4MdlIm9a4Rqu9RT0sgquom6cQvhwlA+HWYgbopP6TxGrVNE45mfTST7I6/sI5psvQDBFogKsKoH7fmpN/uELAEz7PaHrgBx9Hj1+E/X4h1t63L+HHvc7osc2yNl1MIkq4CdpYv5kRf7xC5BLm+i5h3kcwbwLsYMvADFEMdGl7NBE2SeH7PALgMwkgrfWjz29vzj6AiBzieWtwWNP4DB+LSfXo7K44TN+jD7jAAn3okdS4eG86UHA9yag0yyWzmLpk1h6hETu98Z3O5lp0327JPMWH2rP7+2imBJhwRW75aXYfdZ7s1BW2cjn5gPJHuZL7xjog90pTJfkdOUnuleW2GjS4A6MMrf2K7ZfEIjLxAv428Jz+yyw4du7AadZNvWbMH8rfpulReUP1Va3AbaH96Q78CJG0XMX0dg7gwhG6BeE56g7ePrY5Eb4t8NUIjW3LwjQcacAZY2+M71iBqKvQVjoD3+7hO2q+/o5n83K2Xrv1b/lr378Szotq79+yiWtxPZNlT81kljZCdJGOm+npTKKUdaqg9WMCqukEEooJh8nutoC7INNYB/cH+yDjoEtEmcVl0xZyihXbSTGEoklYNpxKI2zzp/GPw/Yh5vAPrw/2IcdA1smDoBChAXXgjuuWqZgtbDCKE6dNPjzFNufa8E+2gT20f3BPuoY2DwRUnAKEZbCSG1FBFsiHJTWCDwx1jr9OLR2K8bRABR5xzzDF3IaOcgC+rVMZLmVbLmVk+VWRvOMZyjbreZ6nrK0rM/CVtoDyXXS8FR0ZSvRferx3ohaJPOXLDRnBsE0b70gSwScIOy1UIobaWnDYUyiuHLeNxr4TdaxiOYTdKZz8HOgLy2nyjkAqux825BqmAwHqAUWQUSnaBFYSthzI6wUUr4k5EedQx4s0kd5Co7QYg2cjHKPmFBaJxCMWB+ktB5SJChqGVWMWS60e0HQjzsHvT949XGIRGAihZJKtsReAHiA7y9/UclsQ5xUwuBf4UORMOFst3ZQtidR6SYS9YE9gEZ9YJ2JgKBLSgkGxiSVcrq1Ywg3uUHso6U03o7xZ4vtDzYBfvAQwA86BzhLLHNQCETycNAAWTTGywegYK1GQMEoM8/MpW7jffgQvA+7hjdNtLVCS86YRuKYazZ6ADJ8h7SSgm7Rp4jw72JTt+E+egjcR92D22kEOMzHRP6avhDNDSfBJQIjBlJlXNjCe15C9YGtUKqQ5cviukyrPrBbq7NKdNrWstXWTlZbGy1lFwTr0wt8F8X68IxHQnTlzudznAhtKc1PO95lcQbDgnNUihrGHKWsDXdYwrVUBtGOUU5ovAgCrRCBGjhMri1knb2oWPOkc+D7Gy2w245aBPrUJ42nVD7AF04LAzcKkEOkKRMsg2nsC8cavCDsR53D3m+wOzAsZhD7WUNl3IakCZB1BpEh01Y41cg91IRKH98rH0Bq9aKOoTqHPU2k81s6SnLNNWzM4s4rc1pTBbm3FAYpciydIIKRzjK/scMRzHQK/G0o1vJu5Uai9eAzq45tObPEaNBhzbGUxkprbXt05RkyolLhOFWcP9/J1d3wHzwU/oNOwg+YvYHiUisHYiv9N2XjBgaUzkB9hPMHXZa7ZyNgd+N/+FD8D7uIPxwIeJiUDOZNacoZFy3+BqYOpo2DJgjBzON8I2IbRnY3/kcPxf+oi/iH/R5m4Fb8sRdlgpn2fFEoY/zxgDMWhmnu2Z+Noq05+Vpz/rXmFGyrs7A1J2JrzsXWnI6tOSP7/JOy5z4v23QB/WmJ3OfsXj/KiG9uvHG/w2YcJNyJ5tAACqFhbLT29xiMhE1a8AnNpGLWOOtdsuhUWLUVl+sU/jRQZi4lqDFIspCmPbSh8LpwyUKB45n2ci9CWhgjzuGNqZAviVCMOgg+OLMD6hzRjeECWqAXXtdSQ8EfoADgza697cqkltxYQTlIh9AviU2PO7gA/lwYwT2ifgT3cK7wtfOdJGaYv0YlNYMOGD43P8oa4zz6DJVMpxZge1bXbpXevj709j7B1NvOBFAa/oJb5SjYNlXGueaLf4YxAdomuDZMP9K3ALdnb5thfncfmN91CGbhYI6k9xdMNc5CJMYZISQFh3OSP9K3prfnaJtR/uk+KP/UGZRtYq3gznJhERWFc5lwWqOp1sb4LT5/H/rZhPnoUzAf3wfm487AbBKEN8xY6v2vliLaDJ04yyysv7BUsCc58V1PuN5GeN9F6vNTpDvHmwgUj6XzWPpjLH0aCdHkQSSI/1kXBZ+B+uSPcVnnkc6uHJMUAuYgdEZQK9stfGYUQnFvXimUXzTq7W8TSuUNrvaP9UsiPB87gzpCakuBqfBkB0jTxfcWpbWUgn5SF05P4te2E24YHvk7H4Yz95KIzml3QPe3ZxQTDvLLmGLNd7hZIigNN2QVRQQNOxtja24SCr9HtWPMh3DsJYn6pDOog7oYCpoI6RWwJrr5kh9NnIE/sw5E31AtmiiNJwialWFWM+fPZ7t1Nr67/L8U+Xz7X4t+839QSwcIzSiTuB4NAAAKVQAAUEsBAhQAFAAICAgA3GY0QkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADcZjRCzSiTuB4NAAAKVQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAALYNAAAAAA==" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1339" height="690" version="4.2" ggbBase64="UEsDBBQACAgIANxmNEIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADcZjRCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1c23LbNhq+Tp8Co4u9immcD127nTat7aRut7Pp7uzsTYaSaImxTGpF+tTp4+yb7IvtB4DUwZYc2bFdOk4cCCSOH/7TB0DZ+/bqbEIuslmVl8V+jyW0R7JiUA7zYrTfO69Pdmzv22++2htl5Sjrz1JyUs7O0nq/JxPeW9RDLmHcV86H+z1KM6szLXdsNtQ7klm3Y41Od6hx/fREpQPKdY+Qqyr/uih/Sc+yapoOsveDcXaWHpeDtA5tjut6+vXu7uXlZdL2npSz0e5o1E+uqmGPYORFtd9rPnyN5lYqXYpQnFPKdv/183FsficvqjotBlmP+Fmd59989WrvMi+G5SW5zIf1GBgIjdGNs3w0xjwNtz2y60tNMdlpNqjzi6xC3aVsmHR9Nu2FYmnh37+Kn8hkPp8eGeYX+TCbAaCEKWGEUNwqRRXjUvVIOcuzom4Ks6bT3ba5vYs8u4zt+k+hS0mdwSLkVd6fZPu9k3RSYV55cTIDphjR7BzZqr6eZP101uYXA2Kv8QcF8t8z3xYWLwKx3xNCvLbutaH0NcYXh7Lcb4/UZTkJjVKiHPnjD8Ipp+S1T1hMOBKt4ysan1EREx4TGRMVy8hYXcaiMpaRsYwUd0yzyW+ep1jMklO1mCXD9Pyvxm+Y/o1p2qVpMj+HPwjzgw+JIH7YLAzfJ7LJ6pg1IWE0Jqx5af0/AS59nwk1D5ZXTrQzYsvr9qkZsaVeI0rbozjHkAnhtu+Sf9bKLWa5Zt242jDLzwR33qlaghZ9hb/h91aX4rOm+ZAetfwczX9Ah4auaH2r8jFlTXoXDI82qL3d1hbuNQMi1diXbUS6zs4qP0Thgm0ijCgorzYwJYowh8R4JeaEKSIVsswS7VNDhNdbSQSxxJdjggQLpCz+kUGnNVFoyz80UbmJkEQJwoLdkgQokGD7gAkXKKEUUajke2e+W6GJ1MgISyQG6K2e8aZFoB7y6JwTwYjwdZkhXBPNifGWk0lvULX1Y0ejnGhKtK8K0wmzGU0malgi/GygBdOyyufgjrPJdL4qAce8mJ7XK9gNzobtx7q8UXpYDk6/v4F1llZ1+xmF4K4WXjG6rxWn+WpvkvazCWKL914MCLlIJ17LQ/snZVGTVgR4fDaapdNxPqjeZ3WNWhX5mF6kx2mdXR2gdNUOMHQdnPledj6Y5MM8Lf4JGfFN+AbJwrd729X6dqWbrgdlORu+v64gOeTq39mshH4Jmrjlnx65jm+4UAlf/vFWapB6ked89Q2Dkl5veEdl7Du7mE8uvcqqFs3RzCtdg7/PvK2+LyeLR9MyL+o36bQ+n4VQDYOY+Vl9V4wmWUA32F4EPYPTfnn1vjHdsa3frqfI0TiA/uhNOSlnBCrJFczsqEn7MQ1l/MjmpWgoQ0MJ2q5TPpy/Z46HEiHtxzSUwsLHoTUzZe00GW27yasYQfZWxCxIjY+gzou8Pm4zdT44bWbKYvlfzs/6ELim2mqT7JGa3Nu9IWJ7p9msyCZRjgqs5Hl5XkXJnkvnq73zKvs1rcffFcO/ZyOo5K+pt4o1mo5FFyMeZoP8DBXj8wa61C/rPzDU+HSYjWZZO8NJiI0jsOEtXZbqW49DUwez8uxtcfEbZObGUPd22/nsVYNZPvWiSfow06fZQvqGeZXCyA+X62HyFWYx8AYHQNYexB5Jz+txOQvRL9TWR2Dk3f/+WxTZDJYS8uhVdpKdIfIldZDKINjz9fkuxNR+IUjZ/whDcmP9FrDh9VoJDbKcTqbj1MfdDQaT9BoDWEYltPdzObyJFZYiTAi2YRqFYpplUZziePFhiuaCEi6tdwC/Ilf7vR2dGCjCtWdJDkb590izIqfwk/W6uWIJ49MbCwe5izh9ArHvvwDEeGJ1QGyHJYo/CmSD8uwsLYakCLHIMSxRb+ECU+oljaTMwxexOa/bF2lsqmngFvreqM3BTT8B/tJ0N6FPH479AkGdSBsAFAFJ4MdlIm9a4Rqu9RT0sgquom6cQvhwlA+HWYgbopP6TxGrVNE45mfTST7I6/sI5psvQDBFogKsKoH7fmpN/uELAEz7PaHrgBx9Hj1+E/X4h1t63L+HHvc7osc2yNl1MIkq4CdpYv5kRf7xC5BLm+i5h3kcwbwLsYMvADFEMdGl7NBE2SeH7PALgMwkgrfWjz29vzj6AiBzieWtwWNP4DB+LSfXo7K44TN+jD7jAAn3okdS4eG86UHA9yag0yyWzmLpk1h6hETu98Z3O5lp0327JPMWH2rP7+2imBJhwRW75aXYfdZ7s1BW2cjn5gPJHuZL7xjog90pTJfkdOUnuleW2GjS4A6MMrf2K7ZfEIjLxAv428Jz+yyw4du7AadZNvWbMH8rfpulReUP1Va3AbaH96Q78CJG0XMX0dg7gwhG6BeE56g7ePrY5Eb4t8NUIjW3LwjQcacAZY2+M71iBqKvQVjoD3+7hO2q+/o5n83K2Xrv1b/lr378Szotq79+yiWtxPZNlT81kljZCdJGOm+npTKKUdaqg9WMCqukEEooJh8nutoC7INNYB/cH+yDjoEtEmcVl0xZyihXbSTGEoklYNpxKI2zzp/GPw/Yh5vAPrw/2IcdA1smDoBChAXXgjuuWqZgtbDCKE6dNPjzFNufa8E+2gT20f3BPuoY2DwRUnAKEZbCSG1FBFsiHJTWCDwx1jr9OLR2K8bRABR5xzzDF3IaOcgC+rVMZLmVbLmVk+VWRvOMZyjbreZ6nrK0rM/CVtoDyXXS8FR0ZSvRferx3ohaJPOXLDRnBsE0b70gSwScIOy1UIobaWnDYUyiuHLeNxr4TdaxiOYTdKZz8HOgLy2nyjkAqux825BqmAwHqAUWQUSnaBFYSthzI6wUUr4k5EedQx4s0kd5Co7QYg2cjHKPmFBaJxCMWB+ktB5SJChqGVWMWS60e0HQjzsHvT949XGIRGAihZJKtsReAHiA7y9/UclsQ5xUwuBf4UORMOFst3ZQtidR6SYS9YE9gEZ9YJ2JgKBLSgkGxiSVcrq1Ywg3uUHso6U03o7xZ4vtDzYBfvAQwA86BzhLLHNQCETycNAAWTTGywegYK1GQMEoM8/MpW7jffgQvA+7hjdNtLVCS86YRuKYazZ6ADJ8h7SSgm7Rp4jw72JTt+E+egjcR92D22kEOMzHRP6avhDNDSfBJQIjBlJlXNjCe15C9YGtUKqQ5cviukyrPrBbq7NKdNrWstXWTlZbGy1lFwTr0wt8F8X68IxHQnTlzudznAhtKc1PO95lcQbDgnNUihrGHKWsDXdYwrVUBtGOUU5ovAgCrRCBGjhMri1knb2oWPOkc+D7Gy2w245aBPrUJ42nVD7AF04LAzcKkEOkKRMsg2nsC8cavCDsR53D3m+wOzAsZhD7WUNl3IakCZB1BpEh01Y41cg91IRKH98rH0Bq9aKOoTqHPU2k81s6SnLNNWzM4s4rc1pTBbm3FAYpciydIIKRzjK/scMRzHQK/G0o1vJu5Uai9eAzq45tObPEaNBhzbGUxkprbXt05RkyolLhOFWcP9/J1d3wHzwU/oNOwg+YvYHiUisHYiv9N2XjBgaUzkB9hPMHXZa7ZyNgd+N/+FD8D7uIPxwIeJiUDOZNacoZFy3+BqYOpo2DJgjBzON8I2IbRnY3/kcPxf+oi/iH/R5m4Fb8sRdlgpn2fFEoY/zxgDMWhmnu2Z+Noq05+Vpz/rXmFGyrs7A1J2JrzsXWnI6tOSP7/JOy5z4v23QB/WmJ3OfsXj/KiG9uvHG/w2YcJNyJ5tAACqFhbLT29xiMhE1a8AnNpGLWOOtdsuhUWLUVl+sU/jRQZi4lqDFIspCmPbSh8LpwyUKB45n2ci9CWhgjzuGNqZAviVCMOgg+OLMD6hzRjeECWqAXXtdSQ8EfoADgza697cqkltxYQTlIh9AviU2PO7gA/lwYwT2ifgT3cK7wtfOdJGaYv0YlNYMOGD43P8oa4zz6DJVMpxZge1bXbpXevj709j7B1NvOBFAa/oJb5SjYNlXGueaLf4YxAdomuDZMP9K3ALdnb5thfncfmN91CGbhYI6k9xdMNc5CJMYZISQFh3OSP9K3prfnaJtR/uk+KP/UGZRtYq3gznJhERWFc5lwWqOp1sb4LT5/H/rZhPnoUzAf3wfm487AbBKEN8xY6v2vliLaDJ04yyysv7BUsCc58V1PuN5GeN9F6vNTpDvHmwgUj6XzWPpjLH0aCdHkQSSI/1kXBZ+B+uSPcVnnkc6uHJMUAuYgdEZQK9stfGYUQnFvXimUXzTq7W8TSuUNrvaP9UsiPB87gzpCakuBqfBkB0jTxfcWpbWUgn5SF05P4te2E24YHvk7H4Yz95KIzml3QPe3ZxQTDvLLmGLNd7hZIigNN2QVRQQNOxtja24SCr9HtWPMh3DsJYn6pDOog7oYCpoI6RWwJrr5kh9NnIE/sw5E31AtmiiNJwialWFWM+fPZ7t1Nr67/L8U+Xz7X4t+839QSwcIzSiTuB4NAAAKVQAAUEsBAhQAFAAICAgA3GY0QkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADcZjRCzSiTuB4NAAAKVQAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAALYNAAAAAA==" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | Perfekt, es hat geklappt. | ||
| + | |||
| + | Zur Erklärung: ich habe zunächst das braune Viereck an DC gespiegelt und das rosane Viereck erhalten, dies wiederum an AB gespiegelt und das schwarze Viereck erhalten. | ||
| + | Bei der anderen Verkettung habe ich zunächst an AB gespiegelt und das grüne Viereck erhalten um dieses bei der zweiten Spiegelung an DC auf das rote Viereck zu spiegel.... Ich hoffe einigermaßen nachvollziehbar....--[[Benutzer:Hakunamatata|Hakunamatata]] 12:59, 20. Jan. 2013 (CET) | ||
Version vom 20. Januar 2013, 12:59 Uhr
Was ändert sich, wenn man die Reihenfolge bei der Verkettung zweier Achsenspiegelungen mit einem gemeinsamen Schnittpunkt vertauscht?
Also ich habe mal versucht es anhand eines Geogebra deutlich zu machen, ob es mir gelungen ist kann ich schlecht sagen! Hier ist auf jeden Fall der link:
http://wikis.zum.de/geowiki/Datei:Zusatz_10.pdf
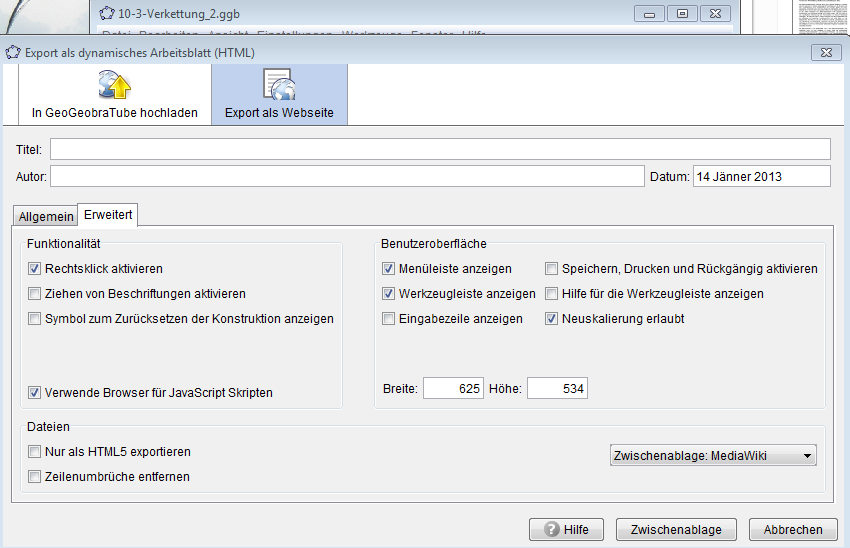
- das Problem ist, dass ich aus dem Bild nicht sehen kann, was du wie gespiegelt hast. Hast du denn auch schon ein Fazit aus deiner Applikation? Oder könntest du die Applikation als Geogebradatei einstellen? (Unter Datei> Export>dynamisches Arbeitsblatt., dann Umstellen unter "Export als Webseite" : Zwischenablage: MediaWiki -> siehe im Bild. )
alles klar, was muss ich machen, wenn das erledigt ist :-D :-D ?!?!?--Hakunamatata 18:15, 19. Jan. 2013 (CET)
- Du muss die Übungsseite öffnen und auf bearbeiten gehen. Dann mit STRG + V, die in der Zwischenablage gespreicherte Datei einfügen. Nicht erschrecken, dass gibt dann ein unverständlichen Text, aber das Ergebnis kannst du dann bei Vorschau sehen.--Tutorin Anne 12:51, 20. Jan. 2013 (CET)
Hier kann es jeder alternativ mal selbst versuchen:
http://wikis.zum.de/geowiki/Verkettung_zweier_Geradenspiegelungen_WS_12_13
--Tutorin Anne 19:05, 18. Jan. 2013 (CET)
Perfekt, es hat geklappt.
Zur Erklärung: ich habe zunächst das braune Viereck an DC gespiegelt und das rosane Viereck erhalten, dies wiederum an AB gespiegelt und das schwarze Viereck erhalten. Bei der anderen Verkettung habe ich zunächst an AB gespiegelt und das grüne Viereck erhalten um dieses bei der zweiten Spiegelung an DC auf das rote Viereck zu spiegel.... Ich hoffe einigermaßen nachvollziehbar....--Hakunamatata 12:59, 20. Jan. 2013 (CET)