Lösung Aufgabe 1.08 soSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgrou…“) |
(→Lösung User ...) |
||
| Zeile 13: | Zeile 13: | ||
=Lösung User ...= | =Lösung User ...= | ||
| + | Ellipsen lassen sich auch als Kegelschnitte definieren. Es sei LaTeX: K ein Kegel mit dem Öffnungswinkel LaTeX: %5Calpha und der Spitze LaTeX: S. Seine Rotationsachse LaTeX: R möge senkrecht auf der Ebene LaTeX: %5Cvarepsilon_0 stehen. Es sei LaTeX: %5Cvarepsilon eine zweite Ebene, die LaTeX: K schneidet. | ||
| + | Ergänzen Sie: | ||
| + | Definition | ||
| + | |||
| + | Wenn LaTeX: %5Cvarepsilon K schneidet, ohne dass LaTeX: %5Cvarepsilon_0 geschnitten wird, dann ist der Schnitt von LaTeX: %5Cvarepsilon mit LaTeX: K eine Ellipse. --[[Benutzer:Bushaltefolie|Bushaltefolie]] 11:44, 14. Mai 2013 (CEST) | ||
=Lösung User ...= | =Lösung User ...= | ||
Version vom 14. Mai 2013, 10:44 Uhr
|
AufgabeEllipsen lassen sich auch als Kegelschnitte definieren. Es sei Definition Wenn ... , dann ist der Schnitt von Lösung User ...Ellipsen lassen sich auch als Kegelschnitte definieren. Es sei LaTeX: K ein Kegel mit dem Öffnungswinkel LaTeX: %5Calpha und der Spitze LaTeX: S. Seine Rotationsachse LaTeX: R möge senkrecht auf der Ebene LaTeX: %5Cvarepsilon_0 stehen. Es sei LaTeX: %5Cvarepsilon eine zweite Ebene, die LaTeX: K schneidet. Ergänzen Sie: Definition Wenn LaTeX: %5Cvarepsilon K schneidet, ohne dass LaTeX: %5Cvarepsilon_0 geschnitten wird, dann ist der Schnitt von LaTeX: %5Cvarepsilon mit LaTeX: K eine Ellipse. --Bushaltefolie 11:44, 14. Mai 2013 (CEST) Lösung User ...Lösung User ... |
ein Kegel mit dem Öffnungswinkel 
und der Spitze 
. Seine Rotationsachse 
möge senkrecht auf der Ebene
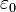stehen. Es sei 
eine zweite Ebene, die 
