Lösung von Aufgabe 4.01 S SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung User ...) |
(→Lösung User ...) |
||
| Zeile 13: | Zeile 13: | ||
Innenwinkelsumme Vierecke: \alpha + \beta + \gamma + \delta = 360° | Innenwinkelsumme Vierecke: \alpha + \beta + \gamma + \delta = 360° | ||
| − | Beweis: | + | <br /> |
| − | (1) aus dem Viereck <math>ABCD</math> kann man die beiden Dreicke D1 <math>ABC</math> und D2 <math>ACD</math> bilden. | + | Beweis:<br /> |
| − | (2) D1 = 180° | + | <br /> |
| − | + | (1) aus dem Viereck <math>ABCD</math> kann man die beiden Dreicke D1 <math>ABC</math> und D2 <math>ACD</math> bilden.<br /> | |
| + | (2) D1 = 180° ;D2 = 180° (durch die IWS beim Dreieck)<br /> | ||
(3) D1 + D2 = 360° | (3) D1 + D2 = 360° | ||
Version vom 1. Juni 2013, 07:17 Uhr
Aufgabe 4.01Der Innenwinkelsatz für Dreiecke sei bereits bewiesen. Lösung User ...Innenwinkelsumme Dreiecke: \alpha + \beta + \gamma = 180° Innenwinkelsumme Vierecke: \alpha + \beta + \gamma + \delta = 360°
Lösung User ...Lösung User ...zurück zu Serie 4 SoSe 2013 |
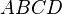 kann man die beiden Dreicke D1
kann man die beiden Dreicke D1 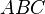 und D2
und D2 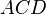 bilden.
bilden.
