Lösung von Aufgabe 4.01 S SoSe 13
Aufgabe 4.01Der Innenwinkelsatz für Dreiecke sei bereits bewiesen. Lösung User ...Innenwinkelsumme Dreiecke:
Kommentar--*m.g.* 23:01, 3. Jun. 2013 (CEST)Der Beweis ist korrekt. Lediglich bei den Formulierungen würde der Mathematiker Anstoß nehmen: Sie haben die Dreiecke Jedem Vieleck kann seine Innenwinkelsumme zugeordnet werden. Wir wollen diese Funktion (Zuordnung) (2) IWS(D1) = 180° ;IWS(D2) = 180° (durch die IWS beim Dreieck) Lösung User ...Lösung User ...zurück zu Serie 4 SoSe 2013 |
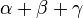 = 180°
Innenwinkelsumme Vierecke:
= 180°
Innenwinkelsumme Vierecke: 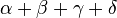 = 360°
= 360°
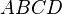 kann man die beiden Dreicke D1
kann man die beiden Dreicke D1 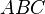 und D2
und D2 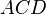 bilden.
bilden.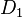 bzw.
bzw. 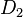 genannt. Damit ist klar, dass es sich um zwei Dreiecke handelt. Dreiecke sind Mengen, die aus drei Strecken bestehen. Die Summe der Größen der Innenwinkel ist eine reelle Zahl. Damit ist die Formulierung
genannt. Damit ist klar, dass es sich um zwei Dreiecke handelt. Dreiecke sind Mengen, die aus drei Strecken bestehen. Die Summe der Größen der Innenwinkel ist eine reelle Zahl. Damit ist die Formulierung 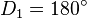 nicht konsistent.
nicht konsistent.
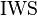 nennen:
nennen:
