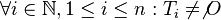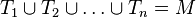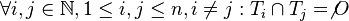Serie 6 SoSe 2013: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6.04) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6.04) |
||
| Zeile 40: | Zeile 40: | ||
# <math>\forall i \in \mathbb{N}, 1 \leq i \leq n: T_i \not= \not O</math> | # <math>\forall i \in \mathbb{N}, 1 \leq i \leq n: T_i \not= \not O</math> | ||
# <math>T_1 \cup T_2 \cup \ldots \cup T_n = M</math> | # <math>T_1 \cup T_2 \cup \ldots \cup T_n = M</math> | ||
| + | # <math>\forall i,j \in \mathbb{N}, 1 \leq i,j \leq n, i \not= j: T_i \cap T_j = \not O</math> | ||
[[Lösung von Aufgabe 6.04 S SoSe 13]]<br /> | [[Lösung von Aufgabe 6.04 S SoSe 13]]<br /> | ||
Version vom 1. Juni 2013, 18:01 Uhr
|
Aufgabe 6.01Lena aus der 5a erklärt Ihnen, was eine Strecke ist: Strecken sind Teile von Geraden. Mein Papa hat mir gesagt, dass die Mathematiker nicht einfach so Teil sondern Teilmenge sagen. Und zu einer Festlegung sagen sie Definition. Ich definiere also:
Aufgabe 6.02Im Folgenden sind wieder formal korrekte Definitionen verlangt. Zur Verfügung steht Ihnen dazu nur die bisher aufgebaute axiomatische Theorie der Geometrie.
Aufgabe 6.03Definieren Sie den Begriff Halbgerade
Aufgabe 6.04Es seien Lösung von Aufgabe 6.04 S SoSe 13 Aufgabe 6.05Lösung von Aufgabe 6.05 S SoSe 13 Aufgabe 6.06Lösung von Aufgabe 6.06 S SoSe 13
Aufgabe 6.07Lösung von Aufgabe 6.07 S SoSe 13 Aufgabe 6.08Lösung von Aufgabe 6.08 S SoSe 13 Aufgabe 6.09
Aufgabe 6.10 |
 und Halbgerade
und Halbgerade  .
.
 eine Menge und
eine Menge und 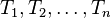 Teilmengen von
Teilmengen von