Lösung von Aufgabe 7.08 S SoSe 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Teilt man einen Kreis durch eine Gerade,welche durch seinen Mittelpunkt geht, so entstehen zwei kongruente Halbkreise. Man kann den Halbkreis auch als Kreisaussc…“)
 
 
Zeile 1: Zeile 1:
 
Teilt man einen Kreis durch eine Gerade,welche durch seinen Mittelpunkt geht, so entstehen zwei kongruente Halbkreise.  
 
Teilt man einen Kreis durch eine Gerade,welche durch seinen Mittelpunkt geht, so entstehen zwei kongruente Halbkreise.  
 
Man kann den Halbkreis auch als Kreisausschnitt sehen,der einen  Winkel von 180° besitzt, und als Sehne den Durchmesser besitzt. --[[Benutzer:Laleoba|Laleoba]] 12:24, 13. Jun. 2013 (CEST)
 
Man kann den Halbkreis auch als Kreisausschnitt sehen,der einen  Winkel von 180° besitzt, und als Sehne den Durchmesser besitzt. --[[Benutzer:Laleoba|Laleoba]] 12:24, 13. Jun. 2013 (CEST)
 +
 +
 +
 +
<u>Alternative:</u>
 +
 +
Sei k ein Kreis mit Mittelpunkt M und g eine Gerade durch M (<math>M\in g</math> ). Die Schnittpunkte von der Geraden mit dem Kreis seien S und S' (<math>\ g \cap k</math> = {S,S'}).
 +
Desweiteren sei Punkt A <math>\in</math> k gegeben mit A <math>\not\in</math> g.
 +
 +
<math>\ 1.Halbkreis := \{P\in k|\overline{AP} \cap g \neq \phi  \}
 +
</math>
 +
<math>\ 2.Halbkreis := \{Q\in k|\overline{AQ} \cap g = \phi  \} \cup \{S,S'\}
 +
</math>
 +
 +
--[[Benutzer:Illu13|Illu13]] 22:23, 13. Jun. 2013 (CEST)

Aktuelle Version vom 13. Juni 2013, 21:23 Uhr

Teilt man einen Kreis durch eine Gerade,welche durch seinen Mittelpunkt geht, so entstehen zwei kongruente Halbkreise. Man kann den Halbkreis auch als Kreisausschnitt sehen,der einen Winkel von 180° besitzt, und als Sehne den Durchmesser besitzt. --Laleoba 12:24, 13. Jun. 2013 (CEST)


Alternative:

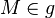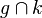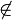Sei k ein Kreis mit Mittelpunkt M und g eine Gerade durch M (M\in g ). Die Schnittpunkte von der Geraden mit dem Kreis seien S und S' (\ g \cap k = {S,S'}). Desweiteren sei Punkt A \in k gegeben mit A \not\in g.

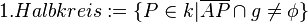
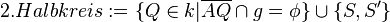
\ 1.Halbkreis := \{P\in k|\overline{AP} \cap g \neq \phi \} \ 2.Halbkreis := \{Q\in k|\overline{AQ} \cap g = \phi \} \cup \{S,S'\}

--Illu13 22:23, 13. Jun. 2013 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_7.08_S_SoSe_13&oldid=23906“