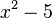Übungen 08: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 2)
(→‎Aufgabe 1)
Zeile 1: Zeile 1:
 
=Aufgabe 1=
 
=Aufgabe 1=
−
Bestimmen Sie die Koordinaten des Vekotrs <math>\vec{x}=\begin{pmatrix} 19 \\ 5 \\ -17 \end{pmatrix}\</math> bezüglich der Basis <math>B=\{\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix};\begin{pmatrix} -4 \\ -5 \\ -6 \end{pmatrix};\begin{pmatrix} 7 \\ 8 \\ 7 \end{pmatrix}\}</math>
+
Bestimmen Sie die Koordinaten des Vekotrs <math>\vec{x}=\begin{pmatrix} 19 \\ 5 \\ -17 \end{pmatrix}\</math> bezüglich des Erzeugendensystem <math>E=\{\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix};\begin{pmatrix} -4 \\ -5 \\ -6 \end{pmatrix};\begin{pmatrix} 7 \\ 8 \\ 7 \end{pmatrix}\}</math>
  
 
==Aufgabe 2==
 
==Aufgabe 2==
Zeile 20: Zeile 20:
  
 
Überprüfen Sie, pb die folgenden 2x2-Matrizen als Linearkombinationen der Matrizen <math>\begin{pmatrix}1 & 0 \\ 1 & 1 \end{pmatrix}</math> und  <math>\begin{pmatrix}1 & 1 \\ 0 & 1 \end{pmatrix}</math> darstellbar sind.<br />
 
Überprüfen Sie, pb die folgenden 2x2-Matrizen als Linearkombinationen der Matrizen <math>\begin{pmatrix}1 & 0 \\ 1 & 1 \end{pmatrix}</math> und  <math>\begin{pmatrix}1 & 1 \\ 0 & 1 \end{pmatrix}</math> darstellbar sind.<br />
−
a) <math>\begin{pmatrix}1 & 2 \\ 3 & 4 \end{pmatrix}</math> <br />
+
 
−
b) <math>\begin{pmatrix}5 & 3 \\ 2 & 5 \end{pmatrix}</math>
+
a) <math>\begin{pmatrix}1 & 2 \\ 3 & 4 \end{pmatrix}</math> <br />
 +
b) <math>\begin{pmatrix}5 & 3 \\ 2 & 5 \end{pmatrix}</math><br />
  
 
==Aufgabe 4==
 
==Aufgabe 4==
  
−
Geben Sie zu folgenden Polynomen die Koordia
+
Geben Sie zu folgenden Polynomen die Koordinaten bezüglich folgendem Erzeugendensystems <math>E=\{p_1(x)=x^2, p_2(x)=x+1, p_3(x)=x^2+x\}</math> an.<br />
 +
 
 +
a) <math>q_1(x)=x^2+5x+3</math><br />
 +
b)<math>q_2(x)=(x-3)^2</math><br />
 +
c)<math>x^2-5</math><br />

Version vom 26. Juni 2013, 14:19 Uhr

Inhaltsverzeichnis

Aufgabe 1

Bestimmen Sie die Koordinaten des Vekotrs Fehler beim Parsen(Lexikalischer Fehler): \vec{x}=\begin{pmatrix} 19 \\ 5 \\ -17 \end{pmatrix}\ 

bezüglich des Erzeugendensystem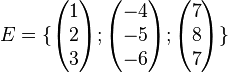 E=\{\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix};\begin{pmatrix} -4 \\ -5 \\ -6 \end{pmatrix};\begin{pmatrix} 7 \\ 8 \\ 7 \end{pmatrix}\}

Aufgabe 2

Wir betrachten in \mathbb{R}^2 die drei Unterräume

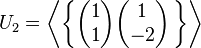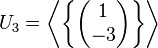Fehler beim Parsen(Lexikalischer Fehler): U_1 = \left\langle \left\{\begin{pmatrix} 1 \\ 2 \end{pmatrix} \right\} \right\rangle\ , U_2 = \left\langle \left\{\begin{pmatrix} 1 \\ 1 \end{pmatrix} \begin{pmatrix} 1 \\ -2 \end{pmatrix} \, \right\} \right\rangle\; und U_3 = \left\langle \left\{\begin{pmatrix} 1 \\ -3 \end{pmatrix} \right\} \right\rangle.

Welche der folgenden Aussagen ist (sind) richtig?

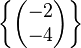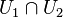  1. Es ist \left\{\begin{pmatrix} -2 \\ -4 \end{pmatrix} \right\} ein Erzeugendensystem von U_1 \cap U_2.
  2. Es ist 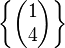\left\{\begin{pmatrix} 1 \\ 4 \end{pmatrix} \right\} eine linear unabhängige Teilmenge von U_2.
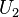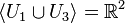  3. Es gilt \langle U_1 \cup U_3 \rangle = \mathbb{R}^2.

Aufgabe 3

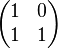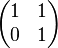Überprüfen Sie, pb die folgenden 2x2-Matrizen als Linearkombinationen der Matrizen \begin{pmatrix}1 & 0 \\ 1 & 1 \end{pmatrix} und \begin{pmatrix}1 & 1 \\ 0 & 1 \end{pmatrix} darstellbar sind.

a) 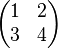\b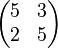egin{pmatrix}1 & 2 \\ 3 & 4 \end{pmatrix}
b) \begin{pmatrix}5 & 3 \\ 2 & 5 \end{pmatrix}

Aufgabe 4

Geben Sie zu folgenden Polynomen die Koordinaten bezüglich folgendem Erzeugendensystems 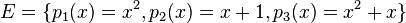E=\{p_1(x)=x^2, p_2(x)=x+1, p_3(x)=x^2+x\} an.

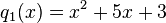
a) q_1(x)=x^2+5x+3
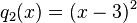
b)q_2(x)=(x-3)^2
c)x^2-5

Von „http://geometrie.zum.de/index.php?title=Übungen_08&oldid=24015“