Lösung von Aufgabe 10.2P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 3: | Zeile 3: | ||
===== Satz VIII.1: (Basiswinkelsatz) ===== | ===== Satz VIII.1: (Basiswinkelsatz) ===== | ||
::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /><br /> | ::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /><br /> | ||
| + | |||
| + | Ich habe den Beweis selbst versucht: | ||
| + | [[Datei:IMG 0002.jpg]] | ||
| + | |||
Beweis:<br /> | Beweis:<br /> | ||
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:34, 2. Jul. 2013 (CEST):<br /> | Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:34, 2. Jul. 2013 (CEST):<br /> | ||
Version vom 2. Juli 2013, 16:59 Uhr
Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Ich habe den Beweis selbst versucht:

Beweis:
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
Behauptung: Die Basiswinkel sind kongruent zueinander: |α| = |β| --Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 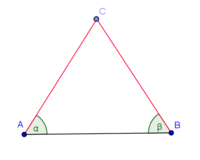
|
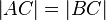
|
Voraussetzung --Nolessonlearned 12:36, 2. Jul. 2013 (CEST) |
| (2) | 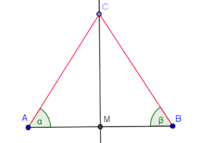
|
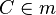 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
(1); Mittelsenkrechtenkriterium --Nolessonlearned 12:37, 2. Jul. 2013 (CEST) |
| (3) | |
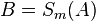
|
Streckentreue bzw Abstanderhaltung der Geradenspiegelung --Nolessonlearned 12:48, 2. Jul. 2013 (CEST) |
| (4) | |
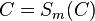
|
C∈m mit m:= Spiegelachse ⇒ C ist Fixpunkt--Nolessonlearned 12:51, 2. Jul. 2013 (CEST) |
| (5) | |
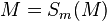
|
M∈m mit m:= Spiegelachse ⇒ M ist Fixpunkt--Nolessonlearned 12:53, 2. Jul. 2013 (CEST) |
| (6) | |
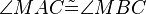
|
Winkeltreue der Geradenspiegelung--Nolessonlearned 12:57, 2. Jul. 2013 (CEST) |

