Lösung von Aufgabe 11.5P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \righ…“) |
(table+) |
||
| Zeile 1: | Zeile 1: | ||
Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | ||
<br /> | <br /> | ||
| − | [[Kategorie:Einführung_P]] | + | [[Kategorie:Einführung_P]]<br /> |
| + | |||
| + | Vor.: | ||
| + | Sa∘Sb∘Sc∘Sd | ||
| + | mit Sa∘Sb ≔ D(S,α) mit a ∩ b = {S} ∧ |∠ab| = α | ||
| + | mit Sc∘Sd ≔ Verschiebung mit c || d --[[Benutzer:Nolessonlearned|Nolessonlearned]] 14:08, 12. Jul. 2013 (CEST)<br /> | ||
| + | |||
| + | Beh.: D(P,α) | ||
| + | mit Sa'∘Sd' ∧ a' ∩ d' = {P} ∧ |∠ab| ≌ |∠a'd'|--[[Benutzer:Nolessonlearned|Nolessonlearned]] 14:08, 12. Jul. 2013 (CEST)<br /> | ||
| + | |||
| + | |||
| + | {| class="wikitable " | ||
| + | ! | ||
| + | ! Beweisschritte | ||
| + | ! Begründung | ||
| + | |- | ||
| + | | 1) | ||
| + | | Sa∘Sb∘Sc∘Sd | ||
| + | | Voraussetzung | ||
| + | |- | ||
| + | | 2) | ||
| + | | Sa'∘Sb' | ||
| + | mit |∠ab| ≌ |∠a'b'| | ||
| + | und b' || c | ||
| + | | (1); Vor.; Winkelkongruenz; | ||
| + | Def. Drehung | ||
| + | |- | ||
| + | | 3) | ||
| + | | Sc'∘Sd' | ||
| + | mit c' = b' (Identität) | ||
| + | mit |cd| = |c'd'| | ||
| + | mit c' || d' | ||
| + | | (2); Vor.; Def. Verschiebung | ||
| + | |- | ||
| + | | 4) | ||
| + | | Sa'∘Sd' ≔ D(P,α) | ||
| + | mit a' ∩ d' = {P} | ||
| + | mit |∠a'd'| = |∠ab| = α | ||
| + | | (1); (2); (3); Vor. | ||
| + | |- | ||
| + | |}--[[Benutzer:Nolessonlearned|Nolessonlearned]] 14:08, 12. Jul. 2013 (CEST) | ||
Version vom 12. Juli 2013, 13:08 Uhr
Zeigen Sie, dass die Verkettung einer Drehung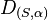 
mit einer Verschiebung wieder eine Drehung 
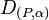ergibt. Wo liegt das neue Drehzentrum P?
Vor.:
Sa∘Sb∘Sc∘Sd
mit Sa∘Sb ≔ D(S,α) mit a ∩ b = {S} ∧ |∠ab| = α
mit Sc∘Sd ≔ Verschiebung mit c || d --Nolessonlearned 14:08, 12. Jul. 2013 (CEST)
Beh.: D(P,α)
mit Sa'∘Sd' ∧ a' ∩ d' = {P} ∧ |∠ab| ≌ |∠a'd'|--Nolessonlearned 14:08, 12. Jul. 2013 (CEST)
| Beweisschritte | Begründung | |
|---|---|---|
| 1) | Sa∘Sb∘Sc∘Sd | Voraussetzung |
| 2) | Sa'∘Sb'
mit |∠ab| ≌ |∠a'b'| und b' || c |
(1); Vor.; Winkelkongruenz;
Def. Drehung |
| 3) | Sc'∘Sd'
mit c' = b' (Identität) mit |cd| = |c'd'| mit c' || d' |
(2); Vor.; Def. Verschiebung |
| 4) | Sa'∘Sd' ≔ D(P,α)
mit a' ∩ d' = {P} mit |∠a'd'| = |∠ab| = α |
(1); (2); (3); Vor. |
