Lösung von Aufgabe 11.5P (SoSe 13)

Zeigen Sie, dass die Verkettung einer Drehung 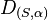$D_{\left( S,\alpha \right) }$ mit einer Verschiebung wieder eine Drehung 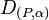$D_{\left( P,\alpha \right) }$ ergibt. Wo liegt das neue Drehzentrum P?

Beweis 1 von Nolessenlearnd

Vor.: Sa∘Sb∘Sc∘Sd
mit Sa∘Sb ≔ D(S,α) mit a ∩ b = {S} ∧ |∠ab| = α
mit Sc∘Sd ≔ Verschiebung mit c || d --Nolessonlearned 14:08, 12. Jul. 2013 (CEST)

Beh.: D(P,α)
mit Sa'∘Sd' ∧ a' ∩ d' = {P} ∧ |∠ab| ≌ |∠a'd'|--Nolessonlearned 14:08, 12. Jul. 2013 (CEST)

	Beweisschritte	Begründung
1)	Sa∘Sb∘Sc∘Sd	Voraussetzung
2)	Sa'∘Sb' mit |∠ab| ≌ |∠a'b'| und b' || c	(1); Vor.; Winkelkongruenz; Eigenschaft der Drehung
3)	Sc'∘Sd' mit c' = b' (Identität) mit |cd| = |c'd'| mit c' || d'	(2); Vor.; Eigenschaft der Verschiebung; Involutorische Abbildung
4)	Sa'∘Sd' ≔ D(P,α) mit a' ∩ d' = {P} mit |∠a'd'| = |∠ab| = α	(1); (2); (3); Vor.; Winkelkongruenz

--Nolessonlearned 14:08, 12. Jul. 2013 (CEST)

So kannst du das beweisen. Allerdings lassen sich die Schritte 2 und 3 nicht aus den Definitionen der Drehung und Verschiebung ableiten, sondern aus Sätzen (z.B. Satz IX. 2). Deshalb musst du Eigenschaften der Drehung bzw. Verschiebung schreiben. Bei Schritt 4 fände ich ganz schön, wenn du noch begründest, warum du Spiegelung an Gerade b' und c' weggelassen hast. Dies ist vielleicht sogar in einem zusätzlichen Schritt vor 4.) übersichtlicher.--Tutorin Anne 16:06, 12. Jul. 2013 (CEST)

• Hallo Anne, erstmal danke für deine Hilfe. Schau dir bitte bei Gelegenheit auch die Zusatzaufgaben an. Bin auf deine Mithilfe angewiesen, da sich meine Lerngruppe aufgelöst hat. So nun zur Aufgabe. Ich dachte das die Erwähnung in Schritt 3, dass b' und c' identisch sind als Begründung ausreichend sei.--Nolessonlearned 16:28, 12. Jul. 2013 (CEST)
  
  • Hallo Nolessonlearned, nur weil zwei Geraden identisch sind, heißt das nicht, dass sie sich in Luft auflösen. Entscheidend ist, dass man die Spiegelungen an den jeweiligen Geraden weglassen kann, aber warum???--Tutorin Anne 17:23, 12. Jul. 2013 (CEST)
    
    • Hallo Anne, ich glaube zu verstehen was du meinst. Wenn zwei Spiegelachsen identisch sind, wird die verkettete Spiegelung involutorisch und dadurch vernachlässigbar.--Nolessonlearned 23:00, 12. Jul. 2013 (CEST)
      

• Ich habe eine Frage dazu, woher wusste man dass man die Verkettung von 4 Geradenspiegelung nehmen muss? Nach dem ich die Fragestellung jetzt 5 mal gelesen habe und mir die Lösung von Nolessonlearned gelesen habe, denke ich, weil eine Drehung 2 Sg hat und weil es zwei mal ist = 4 Verkettungen? Rate ich grad nur???? :-s --Blumenkind 18:31, 12. Jul. 2013 (CEST)Blumenkind 18:27, 12.Juli
  • Hallo Blumenkind, die Verkettung von 4 Geradenspiegelungen in diesem Fall erkennst du daran, dass die Drehung aus 2 sich schneidenden Spiegelachsen und die Verschiebung aus 2 zueinander parallelen Spiegelachsen besteht. Ich hoffe ich konnte mich verständlich ausdrücken.--Nolessonlearned 22:57, 12. Jul. 2013 (CEST)
    
• Warum haben die Winkel in Schritt 4 eigentlich das selbe Maß? Wie kannst du das begründen?--Tutorin Anne 01:07, 14. Jul. 2013 (CEST)
  
  • Danke, ist ergänzt.--Nolessonlearned 14:02, 14. Jul. 2013 (CEST)
    
    • Ich würde es mit dem Stufenwinkelsatz begründen.--Tutorin Anne 10:03, 15. Jul. 2013 (CEST)

Beweis 2 von Blumenkind

Ich gehe davon aus, dass man für diese Aufgabe die Verkettung von 4 Geradenspiegelungen nehmen darf.

• Vor: Geraden a, b, c, d mit a geschnitten b = M und c II d sowie Sa o Sb o Sc o Sd

• Behauptung: ?? ICH WEISS NICHT GENAU, WAS ICH SCHREIBEN SOLL:-///
  • z.B. Die Verkettung Sa o Sb o Sc o Sd entspricht der Drehung um P mit dem Winkel $\alpha$ - dann sollte

$\alpha$ auch in der Voraussetzung ergänzt werden. Oder schreibe es wie Nolessonlearnd oder ähnlich.--Tutorin Anne 01:05, 14. Jul. 2013 (CEST) BEWEIS:
Konstruktion: Ich habe zuerst eine Paralle zur Gerade c gezeichnet die durch den Punkt M verläuft. Die neue Gerade bezeichne ich c`.
Nun kann man sehen dass drei Geraden bzw. die Geraden c´c und d parallel sind eine weitere Gerade d`die ebenso parallel ist
für die gilt Sc o Sd= Sc´o Sd´ Jetzt kann ich diese Formel in die Verkettung von 4 Sg einsetzen:
1. Sa o Sb o Sc o Sd = Sa o Sb o Sc`o Sd`; Siehe Konstruktionsbeschreibung
= (Sa o Sb o Sc`) o Sd`mit a geschnitten b geschnitten c`= (M); Siehe Skizze (leider funktioniert bei mir Geogebra nicht, ich hoffe ihr versteht was ich meine??)
= Se o Sd`; Verkettungen von 3 Sg, die sich in einem Punkt schneiden entsteht eine neue Sg die ich Se genannt habe bzw. Se ersetzt Sa o Sb o Sc´

• Wir haben es noch nicht in der Vorlesung durchgeführt aber weil ich ja NICHTS ZU TUN HABE (*NERD*;-)) habe ich mich bzw. MUSS ICH MICH für die Klausur vorbereiten, da es mein 2. Versuch ist, deshalb bitte nicht sauer werden. Es kann auch falsch sein, was ich gemacht habe. Von daher;-). --Blumenkind 19:54, 12. Jul. 2013 (CEST)Blumenkind 19:51, 12.Juli
  • Super, dass du es nochmal anders beweist. Das geht natürlich ebenfalls. Allerdings musst du jetzt noch begründen, dass der Winkel der ursprünglichen Drehung das selbe Maß wie der der neuen Drehung ist, der Punkt P aber ein andere als M ist. --Tutorin Anne 01:05, 14. Jul. 2013 (CEST)