Lösung von Aufgabe 10.4P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP'…“) |
(table+) |
||
| Zeile 2: | Zeile 2: | ||
Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=S_a\circ S_b(P) </math>.<br /> | Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=S_a\circ S_b(P) </math>.<br /> | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| + | |||
| + | |||
| + | '''Voraussetzung''':<br /> | ||
| + | a ∩ b = {S} ∧ a ⊥ b --[[Benutzer:Nolessonlearned|Nolessonlearned]] 18:24, 13. Jul. 2013 (CEST)<br /> | ||
| + | |||
| + | '''Behauptung''':<br /> | ||
| + | S ist Mittelpunkt von P͞,P͞``<br /> | ||
| + | mit P``= Sa∘Sb(P) --[[Benutzer:Nolessonlearned|Nolessonlearned]] 18:24, 13. Jul. 2013 (CEST)<br /> | ||
| + | |||
| + | |||
| + | {| class="wikitable " | ||
| + | |- style="background: #DDFFDD;" | ||
| + | ! | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | | 1) | ||
| + | | ∃m: m ∩ a ∩ b = {S} | ||
| + | | Voraussetzung; | ||
| + | Konstruktion der Gerade m | ||
| + | |- | ||
| + | | 2) | ||
| + | | ∃Q∈m: Q͞P ≌ Q͞P͞`` | ||
| + | | (1); Mittelsenkrechtenkriterium | ||
| + | |- | ||
| + | | 3) | ||
| + | | m ⊥ P͞P͞`` | ||
| + | | (2); Def. Mittelsenkrechte | ||
| + | |- | ||
| + | | 4) | ||
| + | | S ist Mittelpunkt von P͞P͞`` | ||
| + | | (1); (2); (3); Voraussetzung | ||
| + | |}--[[Benutzer:Nolessonlearned|Nolessonlearned]] 18:24, 13. Jul. 2013 (CEST)<br /> | ||
Version vom 13. Juli 2013, 17:24 Uhr
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 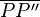 , mit
, mit 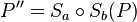 .
.
Voraussetzung:
a ∩ b = {S} ∧ a ⊥ b --Nolessonlearned 18:24, 13. Jul. 2013 (CEST)
Behauptung:
S ist Mittelpunkt von P͞,P͞``
mit P``= Sa∘Sb(P) --Nolessonlearned 18:24, 13. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | ∃m: m ∩ a ∩ b = {S} | Voraussetzung;
Konstruktion der Gerade m |
| 2) | ∃Q∈m: Q͞P ≌ Q͞P͞`` | (1); Mittelsenkrechtenkriterium |
| 3) | m ⊥ P͞P͞`` | (2); Def. Mittelsenkrechte |
| 4) | S ist Mittelpunkt von P͞P͞`` | (1); (2); (3); Voraussetzung |

