Lösung von Zusatzaufgabe 6.1P (SoSe 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie: Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>. [[Kategorie:Einführ…“)
 
(table+)
Zeile 1: Zeile 1:
−
Beweisen Sie: Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>.
+
Beweisen Sie: Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>.<br /><br />
 +
'''Voraussetzung''':<math>Zw(A,B,C)\ mit\ A,B,C\ \in\ E</math> <br /><br />
 +
'''Behauptung''':<math>koll(A,B,C)</math><br /><br />
 +
 
 +
 
 +
{| class="wikitable "
 +
|- style="background: #DDFFDD;"
 +
!
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
| 1)
 +
| <math>\left| AC \right| =\left| AB \right| +\left| BC \right|</math>
 +
| Voraussetzung; Def. Zwischen
 +
|-
 +
| 2)
 +
| <math>\overline{AC}\ ist\ Teilmenge\ von\ AC</math>
 +
| (1); Eigenschaft Gerade
 +
|-
 +
| 3)
 +
| <math>A,B,C\ \in\ \overline{AC}</math>
 +
| (1); Eigenschaft Zwischenrelation
 +
|-
 +
| 4)
 +
| <math>A,B,C\ \in\ AC</math>
 +
| (2); (3)
 +
|-
 +
| 5)
 +
| <math>Element</math>
 +
| (1); (2); (3); (4)
 +
q.e.d.
 +
|}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:30, 18. Jul. 2013 (CEST)
 +
 
  
  
  
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_P]]

Version vom 18. Juli 2013, 20:30 Uhr

Beweisen Sie: Aus \operatorname{Zw} \left( A, B, C \right) folgt \operatorname{koll} \left( A, B, C \right) .

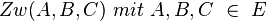
Voraussetzung:Zw(A,B,C)\ mit\ A,B,C\ \in\ E

Behauptung: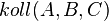koll(A,B,C)


Beweisschritt Begründung
1) 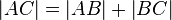\left| AC \right| =\left| AB \right| +\left| BC \right| Voraussetzung; Def. Zwischen
2) 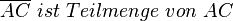\overline{AC}\ ist\ Teilmenge\ von\ AC (1); Eigenschaft Gerade
3) 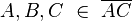A,B,C\ \in\ \overline{AC} (1); Eigenschaft Zwischenrelation
4) 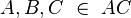A,B,C\ \in\ AC (2); (3)
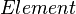
5) Element (1); (2); (3); (4)

q.e.d.


--Nolessonlearned 21:30, 18. Jul. 2013 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_6.1P_(SoSe_13)&oldid=24869“