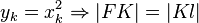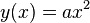Übung 2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Faltkonstruktion der Parabel) |
*m.g.* (Diskussion | Beiträge) (→y(x)=ax^2) |
||
| Zeile 13: | Zeile 13: | ||
<br /> | <br /> | ||
<math>y_k=x_k^2 \Rightarrow |FK|=|Kl|</math> | <math>y_k=x_k^2 \Rightarrow |FK|=|Kl|</math> | ||
| − | ==<math>y(x)=ax^2</math>== | + | ==Parabel: <math>y(x)=ax^2</math>== |
Version vom 16. November 2013, 18:46 Uhr
Inhaltsverzeichnis |
Faltkonstruktion der Parabel
Normalparabel
Es sei 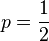 ,
, 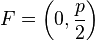 .
.
Die Gerade  sei durch die Gleichung
sei durch die Gleichung 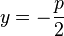 gegeben.
gegeben. 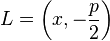 sei ein beliebiger Punkt auf
sei ein beliebiger Punkt auf  .
.
Der Punkt  sei der Schnittpunkt der Mittelsenkrechten
sei der Schnittpunkt der Mittelsenkrechten  von
von 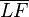 mit der in
mit der in  auf
auf  errichteten Senkrechten
errichteten Senkrechten  .
.
Aufgabe 1
Man beweise:  ist Tangente an die Normalparabel
ist Tangente an die Normalparabel 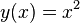 in
in  .
.
Aufgabe 2
Man beweise: 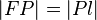 .
.
Aufgabe 3
Gegeben sei der Punkt 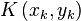 . Man beweise:
. Man beweise: