Lösung von Aufgabe 5.3 P (WS 13/14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 11: | Zeile 11: | ||
Die Relation ist nicht transitiv, weil wenn g schneidet h und h schneidet k nicht unbedingt g k schneiden muss, falls g und k parallel zueinander sind<br /> | Die Relation ist nicht transitiv, weil wenn g schneidet h und h schneidet k nicht unbedingt g k schneiden muss, falls g und k parallel zueinander sind<br /> | ||
--[[Benutzer:Smartie|Smartie]] 15:48, 26. Nov. 2013 (CET) | --[[Benutzer:Smartie|Smartie]] 15:48, 26. Nov. 2013 (CET) | ||
| + | <br/>Doch die isch transitiv, weil wenn ''g'' schneidet ''h'' und ''h'' schneidet ''g'', dann ''g'' schneidet ''g''. Das gilt, weil die Relation reflexiv ist, wie Du richtig festgestellt hast. Symmetrisch isch sie auch. --[[Benutzer:Knöbelspieß|Knöbelspieß]] 22:11, 26. Nov. 2013 (CET)<br/> | ||
Version vom 26. November 2013, 22:11 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
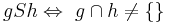
Die Relation ist reflexiv, da g sich selbst schneiden kann (g ist mit sich selbst identisch)
Die Relation ist symmetrisch, weil wenn g schneidet h dann schneidet h auch g
Die Relation ist nicht transitiv, weil wenn g schneidet h und h schneidet k nicht unbedingt g k schneiden muss, falls g und k parallel zueinander sind
--Smartie 15:48, 26. Nov. 2013 (CET)
Doch die isch transitiv, weil wenn g schneidet h und h schneidet g, dann g schneidet g. Das gilt, weil die Relation reflexiv ist, wie Du richtig festgestellt hast. Symmetrisch isch sie auch. --Knöbelspieß 22:11, 26. Nov. 2013 (CET)

