Lösung von Aufgabe 1.3 (WS 16 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
AlanTu (Diskussion | Beiträge) K |
AlanTu (Diskussion | Beiträge) (Meine Lösung hinzugefügt.) |
||
| Zeile 4: | Zeile 4: | ||
<math>M_3: </math> Menge aller gleichwinkligen Dreiecke<br /><br /> | <math>M_3: </math> Menge aller gleichwinkligen Dreiecke<br /><br /> | ||
| + | <popup name="Lösung von AlanTu"> | ||
| + | <math>M_2 = M_3 \subset M_1</math> | ||
| + | <math>\text{Dreieck ist gleichseitig} \iff \text{Dreieck ist gleichwinklig} \Rightarrow \text{Dreieck ist gleichschenklig}</math> | ||
| + | |||
| + | ===Beweis Dreieck ist gleichwinklig ⇒ Dreieck ist gleichseitig=== | ||
| + | |||
| + | Nach dem Innenwinkelsatz müssen alle drei Innenwinkel addiert <math>180^\circ</math> ergeben. Daraus folgt, dass jeder Winkel in einem gleichwinkligen Dreieck <math>\frac{180^\circ}{3} = 60^\circ</math> beträgt. | ||
| + | Nun kann man nachweisen, dass die Seiten gleich lang sind, indem man im Dreieck <math>ABC</math> die Höhe <math>h_c</math> über <math>AB</math> einträgt. Die Strecke zwischen dem Lotfußpunkt und <math>A</math> wird <math>d</math> genannt, die Strecke zwischen Lotfußpunkt und <math>B</math> wird <math>e</math> genannt. Nun gilt <math>tan(60^\circ) = \frac{h_c}{d} = \frac{h_c}{e} \Rightarrow d = e</math>. Dann gilt also auch <math>cos(60^\circ) = \frac{d}{\overline{AC}} \quad\wedge\quad cos(60^\circ) = \frac{e}{\overline{BC}} \iff \frac{1}{2} = \frac{d}{\overline{AC}} \quad\wedge\quad \frac{1}{2} = \frac{e}{\overline{BC}} \iff 2d = \overline{AC} \quad\wedge\quad 2e = \overline{BC} \iff d+e = \overline{AC} \quad\wedge\quad d+e = \overline{BC} \iff \overline{AB} = \overline{AC} \quad\wedge\quad \overline{AB} = \overline{BC}</math>. | ||
| + | |||
| + | ===Beweis Dreieck ist gleichseitig ⇒ Dreieck ist gleichwinklig=== | ||
| + | |||
| + | Man betrachte wieder die Höhe <math>h_c</math> über der Seite <math>AB</math>. Dann gilt in dem Dreieck <math>sin(\alpha) = \frac{h_c}{\overline{AC}} \quad\wedge\quad sin(\beta) = \frac{h_c}{\overline{BC}} \iff sin(\alpha) = \frac{h_c}{\overline{AC}} \quad\wedge\quad sin(\beta) = \frac{h_c}{\overline{AC}} \iff sin(\alpha) = sin(\beta)</math>. Da sowohl <math>\alpha</math> als auch <math>\beta</math> zwischen <math>0^\circ \text{ und } 90^\circ</math> liegen (in einem rechtwinkligen Dreieck sind alle Winkel <math>\leq 90^\circ \text{ und } \geq 0^\circ</math>), kann man daraus schließen, dass <math>\alpha = \beta</math> gilt. Wenn man dieses Vorgehen für alle drei Höhen wiederholt, kann man also zeigen, dass <math>\alpha = \beta = \gamma</math> im gleichseitigen Dreieck gilt. | ||
| + | |||
| + | ===Beweis Dreieck ist gleichseitig ⇒ Dreieck ist gleichschenklig=== | ||
| + | Ein gleichseitiges Dreieck ist per definitionem immer auch gleichschenklig. Ein gleichseitiges Dreieck hat nämlich drei gleich lange Seiten, ein gleichschenkliges erfordert nur zwei. | ||
| + | |||
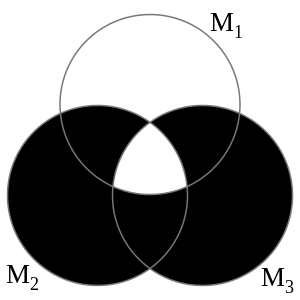
| + | ===Venn-Diagramm=== | ||
| + | |||
| + | [[Datei:WS1617 Loesung Uebung 1-3.svg|300px|Venn-Diagramm]] | ||
| + | |||
| + | (Die Schwarzfärbung von Teilmengen bedeutet, dass diese Teilmengen keine Elemente enthalten, also leere Mengen (<math>\emptyset</math>) sind.) | ||
| + | </popup>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 15:24, 21. Okt. 2016 (CEST) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
[[Kategorie:Lösung zu Übung 1 (Wintersemester 2016/2017)]] | [[Kategorie:Lösung zu Übung 1 (Wintersemester 2016/2017)]] | ||
Version vom 21. Oktober 2016, 14:24 Uhr
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen. Stellen Sie die Teilmengenbeziehungen in einem Venn.Diagramm dar.
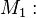 Menge aller gleichschenkligen Dreiecke
Menge aller gleichschenkligen Dreiecke
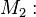 Menge aller gleichseitigen Dreiecke
Menge aller gleichseitigen Dreiecke
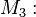 Menge aller gleichwinkligen Dreiecke
Menge aller gleichwinkligen Dreiecke
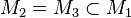
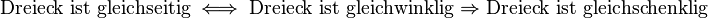
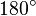 ergeben. Daraus folgt, dass jeder Winkel in einem gleichwinkligen Dreieck
ergeben. Daraus folgt, dass jeder Winkel in einem gleichwinkligen Dreieck 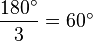 beträgt.
Nun kann man nachweisen, dass die Seiten gleich lang sind, indem man im Dreieck
beträgt.
Nun kann man nachweisen, dass die Seiten gleich lang sind, indem man im Dreieck 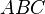 die Höhe
die Höhe 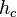 über
über  einträgt. Die Strecke zwischen dem Lotfußpunkt und
einträgt. Die Strecke zwischen dem Lotfußpunkt und  wird
wird  genannt, die Strecke zwischen Lotfußpunkt und
genannt, die Strecke zwischen Lotfußpunkt und  wird
wird  genannt. Nun gilt
genannt. Nun gilt 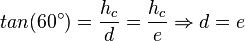 . Dann gilt also auch
. Dann gilt also auch 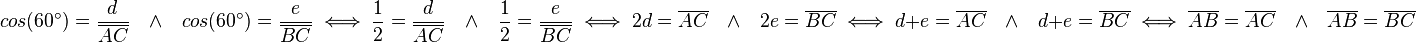 .
.
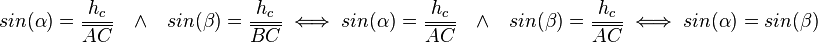 . Da sowohl
. Da sowohl  als auch
als auch  zwischen
zwischen 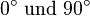 liegen (in einem rechtwinkligen Dreieck sind alle Winkel
liegen (in einem rechtwinkligen Dreieck sind alle Winkel 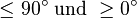 ), kann man daraus schließen, dass
), kann man daraus schließen, dass 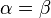 gilt. Wenn man dieses Vorgehen für alle drei Höhen wiederholt, kann man also zeigen, dass
gilt. Wenn man dieses Vorgehen für alle drei Höhen wiederholt, kann man also zeigen, dass 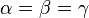 im gleichseitigen Dreieck gilt.
im gleichseitigen Dreieck gilt.
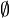 ) sind.)
) sind.)

