Lösung von Aufgabe 1.3 (WS 16 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 34: | Zeile 34: | ||
muss der erste Kreis komplett im zweiten eingebettet sein. Da es sich ja um eine Äquivalenz bzgl. den gleichseitigen und gleichwinkligen Dreiecken | muss der erste Kreis komplett im zweiten eingebettet sein. Da es sich ja um eine Äquivalenz bzgl. den gleichseitigen und gleichwinkligen Dreiecken | ||
handelt müssen folglich auch beide gezeichnete Kreis gleich sein. <br /> | handelt müssen folglich auch beide gezeichnete Kreis gleich sein. <br /> | ||
| − | Gruß Alex | + | Gruß Alex --[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 19:43, 27. Okt. 2016 (CEST) |
Version vom 27. Oktober 2016, 18:43 Uhr
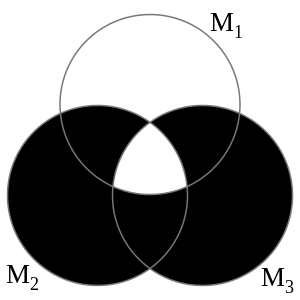
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen. Stellen Sie die Teilmengenbeziehungen in einem Venn.Diagramm dar.
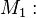 Menge aller gleichschenkligen Dreiecke
Menge aller gleichschenkligen Dreiecke
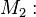 Menge aller gleichseitigen Dreiecke
Menge aller gleichseitigen Dreiecke
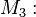 Menge aller gleichwinkligen Dreiecke
Menge aller gleichwinkligen Dreiecke
Hallo AlanTu,
deine Lösung bezüglich der Beziehungen der Mengen ist richtig und auch die Beweise dazu sind schlüssig, super ;) Das Venn-Diagramm ist jedoch nicht ganz richtig. Da es sich um eine echte Teilmengenbeziehung zwischen den gleichseitigen/gleichwinkligen Dreiecken und den gleichschenkligen Dreiecken handelt, muss der erste Kreis komplett im zweiten eingebettet sein. Da es sich ja um eine Äquivalenz bzgl. den gleichseitigen und gleichwinkligen Dreiecken handelt müssen folglich auch beide gezeichnete Kreis gleich sein.
Gruß Alex --Tutor: Alex (Diskussion) 19:43, 27. Okt. 2016 (CEST)
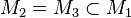
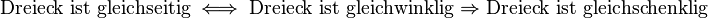
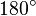 ergeben. Daraus folgt, dass jeder Winkel in einem gleichwinkligen Dreieck
ergeben. Daraus folgt, dass jeder Winkel in einem gleichwinkligen Dreieck 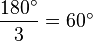 beträgt.
Nun kann man nachweisen, dass die Seiten gleich lang sind, indem man im Dreieck
beträgt.
Nun kann man nachweisen, dass die Seiten gleich lang sind, indem man im Dreieck 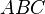 die Höhe
die Höhe 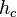 über
über  einträgt. Die Strecke zwischen dem Lotfußpunkt und
einträgt. Die Strecke zwischen dem Lotfußpunkt und  wird
wird  genannt, die Strecke zwischen Lotfußpunkt und
genannt, die Strecke zwischen Lotfußpunkt und  wird
wird  genannt. Nun gilt
genannt. Nun gilt 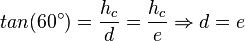 . Dann gilt also auch
. Dann gilt also auch 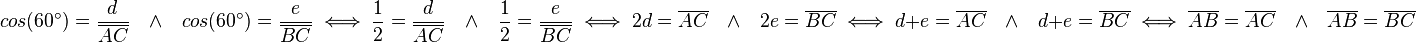 .
.
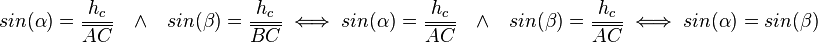 . Da sowohl
. Da sowohl  als auch
als auch  zwischen
zwischen 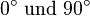 liegen (in einem rechtwinkligen Dreieck sind alle Winkel
liegen (in einem rechtwinkligen Dreieck sind alle Winkel 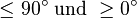 ), kann man daraus schließen, dass
), kann man daraus schließen, dass 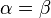 gilt. Wenn man dieses Vorgehen für alle drei Höhen wiederholt, kann man also zeigen, dass
gilt. Wenn man dieses Vorgehen für alle drei Höhen wiederholt, kann man also zeigen, dass 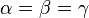 im gleichseitigen Dreieck gilt.
im gleichseitigen Dreieck gilt.
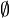 ) sind.)
) sind.)

