Lösung von Aufgabe 1.4 (WS 16 17): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 17: | Zeile 17: | ||
(Diese drei Absätze zeigen nur, dass gilt: <math>S_i \subseteq \{x | x \text{ ist ein Rechteck} \}\text{ für } i \in \{1,2,3\}</math>. Die Umkehrung gilt zwar ebenso, auf den Beweis der Umkehrung verzichte ich an dieser Stelle aber.) | (Diese drei Absätze zeigen nur, dass gilt: <math>S_i \subseteq \{x | x \text{ ist ein Rechteck} \}\text{ für } i \in \{1,2,3\}</math>. Die Umkehrung gilt zwar ebenso, auf den Beweis der Umkehrung verzichte ich an dieser Stelle aber.) | ||
</popup>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 19:47, 24. Okt. 2016 (CEST) | </popup>--[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 19:47, 24. Okt. 2016 (CEST) | ||
| + | |||
| + | Hallo AlanTu, <br /> | ||
| + | deine Lösung ist richtig. Hier eine kleine Anmerkung noch: | ||
| + | Kongruenz meint in diesem Sinne ''deckungsgleich''. <br /> | ||
| + | Kannst du durch eine (Verkettung von) Deckabbildungen / Kongruenzabbildungen, wie Drehung, Spiegelung oder Parallelverschiebung | ||
| + | die Winkel deckungsgleich bekommen? Stichwort: Kongruenz des Winkelmaß und der Seitenlängen. <br /> | ||
| + | Gruß Alex--[[Benutzer:Tutor: Alex|Tutor: Alex]] ([[Benutzer Diskussion:Tutor: Alex|Diskussion]]) 19:48, 27. Okt. 2016 (CEST) | ||
| + | |||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
[[Kategorie:Lösung zu Übung 1 (Wintersemester 2016/2017)]] | [[Kategorie:Lösung zu Übung 1 (Wintersemester 2016/2017)]] | ||
Aktuelle Version vom 27. Oktober 2016, 18:48 Uhr
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen.
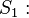Menge aller Vierecke mit vier kongruenten Winkeln
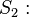Menge aller Vierecke mit gleich langen, einander halbierenden Diagonalen
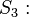Menge aller Vierecke mit zwei Paaren paralleler Gegenseiten und einem rechten Winkel
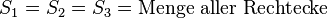
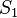: Laut des 
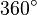, somit hat ein Dreieck mit vier gleich großen Winkeln (
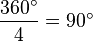, ist also ein Rechteck.
Zu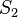 
: Vierecke mit gleich langen sich halbierenden Diagonalen werden von den Diagonalen in vier Dreiecke mit den folgenden Eigenschaften aufgeteilt:
des einen Dreiecks plus den beiden gleich großen Basiswinkeln des anderen Dreiecks 
als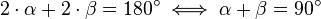 
. Da ein Winkel des großen Dreiecks sich aus 
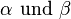zusammensetzt, ist das große Dreieck also ein rechtwinkliges Dreieck. Da das für alle Paarungen von nebeneinanderliegenden Dreiecken gilt, sind die vier Innenwinkel des gesamten Vierecks rechtwinklig
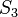: Da das Viereck zwei Paare paralleler Gegenseiten besitzt, ist es also ein Parallelogramm. Im Parallelogramm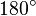 
.
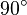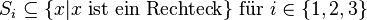. Die Umkehrung gilt zwar ebenso, auf den Beweis der Umkehrung verzichte ich an dieser Stelle aber.)
Hallo AlanTu,
deine Lösung ist richtig. Hier eine kleine Anmerkung noch: Kongruenz meint in diesem Sinne deckungsgleich.
Kannst du durch eine (Verkettung von) Deckabbildungen / Kongruenzabbildungen, wie Drehung, Spiegelung oder Parallelverschiebung die Winkel deckungsgleich bekommen? Stichwort: Kongruenz des Winkelmaß und der Seitenlängen.
Gruß Alex--Tutor: Alex (Diskussion) 19:48, 27. Okt. 2016 (CEST)
