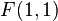Lösung von Aufgabe 13.2P (WS 16/17): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen <math>\varphi_1</math> und <math>\varphi_2</math>, mit <math>\varphi_1\left( \overline{ABC}…“) |
AlanTu (Diskussion | Beiträge) (Meine Lösung hinzugefügt.) |
||
| Zeile 11: | Zeile 11: | ||
<br /> | <br /> | ||
| + | ===Lösung von AlanTu=== | ||
| + | |||
| + | 1. <math>\varphi_1</math> ist eine Translation, <math>\varphi_2</math> eine Drehung | ||
| + | |||
| + | 2. Die roten Geraden <math>s_1: x=3</math> und <math>s_2: x=5</math> bilden <math>\varphi_1</math>, die grünen Geraden (Die Spiegelachsen sind zur besseren Anschauung mit der Maus verschiebbar)<math>s_3: y=x</math> und <math>s_4: y=3</math> bilden <math>\varphi_2</math><ggb_applet style="display:inline-block" width="844" height="538" version="4.0" ggbBase64="UEsDBBQACAgIAIG+OEoAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICACBvjhKAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbOVaXY/bNhZ9Tn8FoYd9im2SomQ59aTwDFo0i6QJMNmi6GKxoCTaw44saiXZYwf98XtJSrLk8cw4Tjx1XCMeSuIlL++5HzxUPP5hNU/QUuSFVOmFQ/rYQSKNVCzT2YWzKKe9wPnh9XfjmVAzEeYcTVU+5+WFw7SkjC+cMBScx8NhL2bTaY+5AvdGfhj2vBELpyTEbBpQB6FVIV+l6hc+F0XGI3Ed3Yg5f6siXhrFN2WZvRoM7u7u+rWqvspng9ks7K+K2EGwzLS4cKqLVzBdZ9Cda8QpxmTw27u3dvqeTIuSp5FwkDZhIV9/92J8J9NY3aE7GZc3YDAZ+Q66EXJ2A0YFZOiggZbKAJFMRKVcigLGtm6N0eU8c4wYT3X/C3uFksYeB8VyKWORXzi4T/whpQwHmPpDzws810EqlyItK2FSKR3U042XUtzZefWVUckcVCqVhFxPif78E1FMMXqpG2IbCo3v2y5sn2HXNtQ2zDaelWF2OLOizMowK8NgjUtZyDARF86UJwVgKNNpDv5r7otynQiznurBxnzyEmwq5CcQdjEEigUdnmP8Un99+DLdMegaSVpay3zxqFLb39JZa7Q+3Vcl/SJD3Vop3WUm9R4w039EqbXrMXAbQ72WTlBl/pnvPY3uY2Zua3wY2f0V+uxZTBwP6lQZV9mBihstW0VPKeaFzhd3hLyRDnuCPMgNfwhR7iEygmZIEWQDIh5iHtySAPm6HSJ3CB0MuShAWo64yCSHF8AfNjST+ciDyfTTIeQkIqCIIc9FxOQUQ5BJyOQl5Ch1QcLzkAeDtHpC9RSuj5gPd26AGKxRp+SQgKALA+Ee1FPkEuTqwWSIqI98PR9hOtX9QC8dpqTIx8gnekLIashom80gHyBXW+NXcMk0W5QdiKJ5XF+WKmt8AdJQjzZlz9anTlV8MU54KBLYKa61JxFa8kRnhFE0VWmJaidS+2yW8+xGRsW1KEsYVaA/+JK/5aVY/QTSRa3byEYqLT7kqrxSyWKeFghFKsHNmlVCWte0WTXcuK0O1u7wWh1+63q4U6+CHrQoBOhXeVGL8zh+oyU2pQGQfJ8m68tc8NtMya4Z44HZdMZiESUyljz9FYJVa9G4oN17kB/QeiUqj6/XBYQwWv0ucgVFhoz6o9YncNDa9rg+7uP2B2YsIq6Tj3XHjDwY9EBX4FvVYtm4iK9EY/0sl3H7+k1xqZK4wcKYf8WzcpEb9gC1Mdc2TdJZIkyImGoLW3N0G6rVtY0N1871cZ3BHbb6w5mBHUFpoB6sd1a1oW2NjF5YI4WNDDYSuA42GTf9ZESNhGlD2xopiF67tMpQUltJcK1GFqagYaeTNib09T6/SGX5tr4pZXRbWUqs/C+LeSiaAOpOSb7SlOPBVoCNb0WeiqSKZ3DkQi0Km56tUI9FJOdwazsqQLh21r9gAfZpLGa5qNedGF5m4TK9uB2p9x6bqX7K1fxNuvwIkbC1gPGgXuW4iHKZ6XhDIewBt2ITU7EsOGwhcXucTkAwPdJbBcBTamgmi+kMEIMi3acfIE8X5Y0Cv08Snn5cwDRQZMBEhv7J0wXsERQD09OJmYg58DBUmujTwdC4ofgvMxRPI45U+AeUvS1HbTwK3VuhWIcr3PEku+GaBlawJHwt8g5QZr53Kt6GD7xjbIQSkBkeCf7PhLCRU1YJgzKY0ORbp4qBRwq0smrRumL2ny6cntusown9EoryLTDPwuRnM7G++FnGsTAbsi0M/0vtkMJGpFhliYxkWUWhRfMpXN1zwLVHtoDFz4+rKbgNbJMvgBU3tfW4sJInYaUVrF4FK6nXYYzVe0aHZtinW6Vn70gkB0FWb0n4a0fiIXFYhyE+Sn7L+QH5Tc8QVe85UI3UfM7TGKXmkPRO5rnKnQ1r57h++O/JSwTR+x8AiVjELZyLspab/INnqvjeaqjmfap+VEP+0iqycQHt8lmMWV0XOh9yhCrRxeXyHOoqOWpZ7QJ2dQ6ANRsR+UqIdZP7g0rWM5VuZffEJvQlNFTjuJ3VwO4TODwRKxZZMQ4NHHrDp3LdKqyd0Ex1aFF72L8tPNsOJvq9J8DtkXsVnnyOhx8Ow0LM9F2zkOiJQPz8hR5czWoa7tYbCjnajmIiJtGh/SYt4ZwozEHp/vHvVohMn7rfpx9znhb6xb6VaR0r9wSanw7QrAK6VyNNyBkBHZ4O0D22zZGCbwro/cnW1VNk6+rzydbVX0C23k+nhSi17zzjuOHeRKzeCLsfeoR98TE/XD7lh8vP98PlaZFe7yvTtL1IRwWBpR7NDe3E9U4a0h4YtQfy5kYTk/28spuetNxzriRlrwg88nLbMRj0g4AMA0ZGQzheUY/+2NP/X7nWlWDU/fgbLrNVGb6dfeAJZnNq3rnHb2Af3vLK2YAfnhr4mvNsv31Ya58whoMRxaPAw9invs2YTzqXviVK9NhG+eNpHeoPOdK7W2ewZ2QuNpA1f3Eb/sIe4i8Hs5jT5DLHeYHyKGHfD+6rQ+G+OkW479FzVtWm50Z/sh/6k0PRn5wi+jteSx8N/Edp/A4yv4PS70Xsd9D7HSR/B9X/csL/t6H9p8Zw6j2y98Ap4PxeXZ6mH3ruhufvPHSR0Rk5ITxNJ9Qv7esyDhnwTYE+aP9Syvwasfpp/ev/A1BLBwiXvZSrwgcAAPcvAABQSwECFAAUAAgICACBvjhKRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAIG+OEqXvZSrwgcAAPcvAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAWggAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | 3. Da <math>\varphi_1</math> eine Translation ist, kann man die beiden Spiegelachsen <math>s_1</math> und <math>s_2</math> um 2 nach links verschieben, ohne die Abbildung zu verändern. Und da <math>\varphi_2</math> eine Drehung ist, können die beiden Spiegelachsen <math>s_3</math> und <math>s_4</math> um 45° gegen den Uhrzeigersinn (im „mathematischen Uhrzeigersinn“) gedreht werden ohne die Abbildung zu verändern. Da dann <math>s_2</math> und <math>s_3</math> deckungsgleich sind und die Spiegelungen an den beiden Achsen direkt nacheinander ausgeführt werden, heben sich die beiden Spiegelungen auf. | ||
| + | |||
| + | 4. Somit kann man die Geraden <math>s_1': x=1</math> und <math>s_4': y=x</math> als Spiegelachsen für die Ersatzabbildung heranziehen. Das entspricht einer Drehung um 90° entgegen dem mathematischen Drehsinn um den Schnittpunkt der beiden Spiegelachsen <math>F(1,1)</math><ggb_applet width="844" height="538" version="4.0" ggbBase64="UEsDBBQACAgIALYAOUoAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAC2ADlKAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbOVb627byBX+nX2KAxbIj8KSZniTlMhZ2MYumiLeBLVbFA2CxZAcSbOmSC2HtKVgX6Dv0QfYZ9hH6ZP0zAxJkZJsK4qdKK6wDi9zZs6c7zs3UtrR94tZDNc8kyJNji3aJRbwJEwjkUyOrSIfdwbW96++G014OuFBxmCcZjOWH1uukhTRsRUEnLGo3+9E7njccR1OOkM/CDre0A3GNCDueGBbAAspXiTpT2zG5ZyF/CKc8hl7k4Ys14qneT5/0evd3Nx0K1XdNJv0JpOgu5CRBbjNRB5b5ckLXK416cbR4jYhtPfP8zdm+Y5IZM6SkFugTCjEq++ejW5EEqU3cCOifIoGU+pbMOViMkWjBrRvQU9JzRGROQ9zcc0lzm1caqPz2dzSYixR48/MGcS1PRZE4lpEPDu2SJf2hzalrj/0HJd4hA4sSDPBk7wUpqXSXrXc6FrwG7OuOtMqXQvyNI0DppaE334Dm9gEjtSBmoONB983Q8TcI4452ObgmoNnZFwz3TWirpFxjYzrWHAtpAhifmyNWSwRQ5GMM+Svvpb5MuZ6P+WNlfn0CG2S4iMKOwQdxYCO9wk5Un8+/rlqoNc2kja05llxp1Iz3tBZaTSc7qrS/ixDnUqpvc1M27vFTP8Opcauu8CtDfUaOlGV/k//bWh07jJzXePtyO6u0He/iImjXhUqozI6QE6VbOk9OZ9JFS/OELyhcnsKGIDg99HLPaBDPPRtwGgA6oHr4SUdgK+OfXD6OOCCAwNQctQBHRzeAP9x+3oxHzxcTN3tY0wCRUUueA5QHVMuYCSBjkuMUdtBCc8DDycp9dRWSzg+uD5eOQNwcY8qJPsUBR2ciNeo3gaHgqMm0z7YPvhqPeqqUPcHauu4pA0+AZ+qBTGqMaJNNKP8ABxljV/CJZJ5kbcgCmdRdZqn85oLlMZ8tEp7Jj+1suKzUcwCHmOluFBMAlyzWEWEVjROkxwqEm1zb5Kx+VSE8oLnOc6S8Au7Zm9Yzhc/orSsdGvZME3kuyzNz9K4mCUSIExjUu85jWnj3K53jRdOY8BtDniNAb9x3t+qN8URKCRH/WkmK3EWRa+VxCo1IJJvk3h5mnF2NU9F24xRTxedES/CWESCJf9AZ1VaFC6wvQb5A7vaSZpFF0uJLgyLf/EsxSRDh91h44OFZGlGHJ90SfODK8qQqeBz23OGHk66ZWjgG9X8uqaILXht/SQTUfP8tTxN46jGQpt/xuZ5kenuAXNjpmw6SSYx1y6isy2W5vAqSBcXxjccs9blco5XxOgPJhp2wNRge7jfSXkMzFHLqI3VUkTLEC1BKmcTUT1Oh7aW0MfAHLUUeq/ZWmkoraykpFIjpE5oxGqFjXZ9VeeLRORvqotchFelpdTI/1TMAl47UHtJ+kBLjnprDja64lnC49KfkcgiLaQJz4arRzwUM7w0AyUgTJH1d9yAuRvxScarfce6LzNw6VHS9NSN23qpH7N09jq5vkRP2NgANmcZegduQmV9M7yyqbJhJMNMzJU3QoAV4oqvPC4SkmGBiZohp8ITFwn1krnIFXAnxXiCeGIK79rvMIqLfJqiV5zELLkscBlMQQiAC39lSYEVxCbYB6qwjfkMuzTItW9q965Z+kH3f4oOSINfMCeusbiiG4e3+qn2aBbPp0z1iCVmMVvyrIWiXu88jdaxrVDD/DA3rjHn3DiV2S+ezHE5HYqtBIdkSVhgfKoWflkeP5rm3zS/ylIVnq2Mbu6usYyuZ0DagCspZjwTYQ1IpAHDmUU5v0O6Vb5pwVg1A7viSBoo0h1RLOVkrFp0mAlsOTqI14wtdKPNAollJ8enFHT+ZPWUYhiu0jZRrCkgfWdYQjnUD1BjseB1okRPEx8xCFnLmFXeybEiXmHbL3VyzMs0qE/+IqKIJ/Vu1zlH9SvaSbfvNabXzDdyRE1UmM5mLIkg0c3Y31J8DuHWqjtgWGeXcAyYmRmWWdvuen/8Dn+Gc7Z4fy6S9xF2Fh+OgHzAcVtFgqGnyKvJ8mfXqCwVbfiGsr5mWEnvH0tVXSD7x9IqIkhJIy0jouPUa+3BF/81MVOkSd98MY9FKPKNuFnMM1xPEVtDgsTi7WNroXiAzjbsm1D27oOY7gVxVXw3A21viGkJMXkUiMXsFojvyOQnh5XJVRL79FzesUtcvYdK5luc0m44pfcATmnvjDwW9UgYkFTDXQpH8N9//wfsr+O33pfw2x0z9WL/TO18UqZ2HouxR0jmHbqWzcmXSOZtxs5FlqXZGmPm5vuTI8C8/MFQp4JhnZyT52yeypd3E7SWy8opXzWjrSiw28+khLhVjmp96CO0n21cTp9CjqcPneLvAOzsKQBWF0X6QIi1g/tdGi8nabIW3ScmoE9Nyj3biGp8Qo95eEWNWGjEGB6cYyu4L9aNwoqEeql9k9rt/DbwbBJMPUdT7NG9H73ucUPJJ+qq3kh4jyN++kY/++mgel7u0EfrAbTHxMq1Xyc5zyTXrzM2X+FccT5Xb87eJpcZS6T6cm79NcquQLPDAdotge7UbyboEwI6OBygO+56Vzv4poDevdk6u6/ZOvv0ZuvsKzRbb8djyXPFnaeJ6+/ciFWFsP2xH6Eu3sXD6X08nH46D6eH1fR6D9ym7dR0lBCY1qO+sFt+vbUNaU4MmxNZfaEak91Y2d6eNOh5qk3KTh74yNtt+uCgOxjQ/sClwz4+Xtme/UNHfce4VJlg2P74q15mLTN8O3Xgns7m0NjZ6G+wDq+x8mTADw4NfNXzrL99WCpOXJcMhjYZDjxCfNs3EfNRxdLTbInKMqEKslMXZPe2grx3WT7M4vw4bwTu7EB3g/tsX7jPDhHujX7TLYPtS6N/shv6J/uif3KI6G95z/po4N/Zl27pTrf0qDt1qlv61S1d65be9fM72P+bPvbQSnb1Q5XOLW3t03sXd5g8dJxV47r1KYIOnxAJwWGSUL2FrtI4RsC3BfrGDwsu+SKvfu/y/NcizV/Kn20osLRgsYYpD3gCUoRTYMX4CCL2/E+UvIwwLxfJRE5iroaUNA5zkWBe59k4jSc8ibpmOb2FNtk56rTaG9iZ4du+2n4+yV/e/t32Z/8WQf9a8p2qyqD8oN8dtmq7U3qF47ae4r1mrW/y0Gv+UFL/VLn8/25e/Q9QSwcIA4IfQjcJAAAUNAAAUEsBAhQAFAAICAgAtgA5SkXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAC2ADlKA4IfQjcJAAAUNAAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAM8JAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> --[[Benutzer:AlanTu|AlanTu]] ([[Benutzer Diskussion:AlanTu|Diskussion]]) 00:29, 25. Jan. 2017 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 25. Januar 2017, 00:29 Uhr
Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen 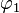 und
und 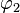 , mit
, mit 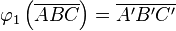 und
und 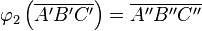 .
.
Hinweis: Der Punkt E hat eine besondere Bedeutung für 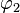 .
.
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
- Um welche Arten von Abbildungen handelt es sich bei
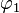 und
und 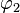 ?
?
- Zeichnen Sie jeweils für
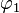 und
und 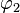 die passende Anzahl von Spiegelachsen in die Skizze ein.
die passende Anzahl von Spiegelachsen in die Skizze ein.
- Wir betrachten nun die Verkettung
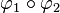 . Durch welche Ersatzabbildung kann diese Verkettung
. Durch welche Ersatzabbildung kann diese Verkettung 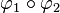 ersetzt werden? (Begründen Sie Ihre Entscheidung).
ersetzt werden? (Begründen Sie Ihre Entscheidung).
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
Lösung von AlanTu
1. 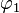 ist eine Translation,
ist eine Translation, 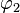 eine Drehung
eine Drehung
2. Die roten Geraden 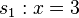 und
und 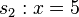 bilden
bilden 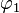 , die grünen Geraden (Die Spiegelachsen sind zur besseren Anschauung mit der Maus verschiebbar)
, die grünen Geraden (Die Spiegelachsen sind zur besseren Anschauung mit der Maus verschiebbar)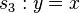 und
und 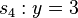 bilden
bilden 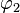
3. Da 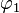 eine Translation ist, kann man die beiden Spiegelachsen
eine Translation ist, kann man die beiden Spiegelachsen 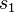 und
und 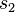 um 2 nach links verschieben, ohne die Abbildung zu verändern. Und da
um 2 nach links verschieben, ohne die Abbildung zu verändern. Und da 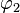 eine Drehung ist, können die beiden Spiegelachsen
eine Drehung ist, können die beiden Spiegelachsen 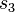 und
und 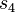 um 45° gegen den Uhrzeigersinn (im „mathematischen Uhrzeigersinn“) gedreht werden ohne die Abbildung zu verändern. Da dann
um 45° gegen den Uhrzeigersinn (im „mathematischen Uhrzeigersinn“) gedreht werden ohne die Abbildung zu verändern. Da dann 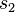 und
und 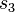 deckungsgleich sind und die Spiegelungen an den beiden Achsen direkt nacheinander ausgeführt werden, heben sich die beiden Spiegelungen auf.
deckungsgleich sind und die Spiegelungen an den beiden Achsen direkt nacheinander ausgeführt werden, heben sich die beiden Spiegelungen auf.
4. Somit kann man die Geraden 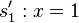 und
und 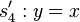 als Spiegelachsen für die Ersatzabbildung heranziehen. Das entspricht einer Drehung um 90° entgegen dem mathematischen Drehsinn um den Schnittpunkt der beiden Spiegelachsen
als Spiegelachsen für die Ersatzabbildung heranziehen. Das entspricht einer Drehung um 90° entgegen dem mathematischen Drehsinn um den Schnittpunkt der beiden Spiegelachsen