Didaktik der Bruchrechnung: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Bruchbegriff) |
*m.g.* (Diskussion | Beiträge) (→gebrochene Zahlen bzw. Bruchzahlen) |
||
| Zeile 5: | Zeile 5: | ||
===Brüche=== | ===Brüche=== | ||
===gebrochene Zahlen bzw. Bruchzahlen=== | ===gebrochene Zahlen bzw. Bruchzahlen=== | ||
| − | Unter einer gebrochenen Zahl versteht man eine | + | Unter einer gebrochenen Zahl versteht man eine Menge von Brüchen, die durch Kürzen oder Erweitern auseinander hervorgehen.<br /> |
| + | |||
| + | |||
| + | Relation: (quotientengleich)<br /> | ||
| + | Zwei Brüche <math>\frac{a}{b}</math> und <math>\frac{c}{d}</math> heißen quotientengleich, wenn<br /> | ||
| + | <math>a \cdot d = b \cdot c</math> gilt. | ||
==Gruppen== | ==Gruppen== | ||
Version vom 21. Februar 2017, 12:33 Uhr
Inhaltsverzeichnis |
Fachliche Grundlagen
Bruchbegriff
Äquivalenzrelationen
Klasseneinteilungen
Brüche
gebrochene Zahlen bzw. Bruchzahlen
Unter einer gebrochenen Zahl versteht man eine Menge von Brüchen, die durch Kürzen oder Erweitern auseinander hervorgehen.
Relation: (quotientengleich)
Zwei Brüche 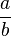 und
und 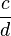 heißen quotientengleich, wenn
heißen quotientengleich, wenn
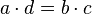 gilt.
gilt.

