Was ist eine Gruppe? SoSe 2017: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Die "übliche" Gruppendefinition (kurze Version))
(→‎Beweis von Satz 1)
Zeile 43: Zeile 43:
 
Übungsaufgabe, Hinweise
 
Übungsaufgabe, Hinweise
 
# Beginnen Sie mit Linksinvers=Rechtsinvers
 
# Beginnen Sie mit Linksinvers=Rechtsinvers
−
# Multiplizieren Sie zunächst das Linksinverse <math>g^-1</math> eines beliebigen Elementes <math>g</math> von rechts mit <math>g</math>:<math>g \odot g^{-1}</math>
+
# Multiplizieren Sie zunächst das Linksinverse <math>g^{-1}</math> eines beliebigen Elementes <math>g</math> von rechts mit <math>g</math>:<math>g \odot g^{-1}</math>
 
# Ersetzen Sie <math>g</math> durch <math>e \odot g</math>
 
# Ersetzen Sie <math>g</math> durch <math>e \odot g</math>
 
# Ersetzen Sie <math>e</math> durch das Produkt des Linksinversen vom Linksinversen von <math>g</math> mit dem Linksinversen von <math>g</math>: <math>(g^{-1})^{-1} \odot g^{-1}</math>.
 
# Ersetzen Sie <math>e</math> durch das Produkt des Linksinversen vom Linksinversen von <math>g</math> mit dem Linksinversen von <math>g</math>: <math>(g^{-1})^{-1} \odot g^{-1}</math>.

Version vom 1. Mai 2017, 13:20 Uhr

Inhaltsverzeichnis

Beispiele für Gruppen

endliche Gruppen

Die Gruppe der Deckabbildungen des Rechtecks

Die Gruppe der Deckabbildungen der Raute

unendliche Gruppen

Gebrochene Zahlen: [\mathbb{Q}^+, \cdot ]

Ganze Zahlen: [\mathbb{Z}, +]

Gegenbeispiele für Gruppen

Gruppendefinitionen

Die "übliche" Gruppendefinition (lange Version)

Definition 1a: (Gruppe Langfassung)

Es sei G eine nichtleere Menge auf der eine Verknüpfung \odot.
Wenn die folgenden Axiome erfüllt sind, heißt die Struktur \mathbb{G}:=[G, \odot ] Gruppe:

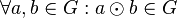
  1. \odot ist auf G abgeschlossen: \forall a,b \in G: a \odot b \in G
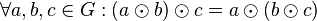
  2. \odot ist assoziativ auf G: \forall a, b, c \in G: (a \odot b) \odot c = a \odot (b \odot c)
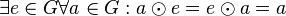  3. Bezüglich \odot existiert in G ein ("universelles") Einslement e: \exist e \in G \forall a \in G: a \odot e = e \odot a= a .
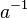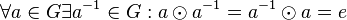  4. Bezüglich \odot existiert zu jedem a aus G ein ("persönliches") inverses Element a^{-1}: \forall a \in G \exist a^{-1} \in G: a \odot a^{-1} = a^{-1} \odot a = e.

Die "übliche" Gruppendefinition (kurze Version)

Definition 1b: (Gruppe, Kurzfassung)

Es sei G eine nichtleere Menge auf der eine Verknüpfung \odot.
Wenn die folgenden Axiome erfüllt sind, heißt die Struktur \mathbb{G}:=[G, \odot ] Gruppe:

  1. \odot ist auf G abgeschlossen: \forall a,b \in G: a \odot b \in G
  2. \odot ist assoziativ auf G: \forall a, b, c \in G: (a \odot b) \odot c = a \odot (b \odot c)
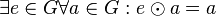  3. Bezüglich \odot existiert in G ein ("universelles") Einslement e: \exist e \in G \forall a \in G: e \odot a= a .
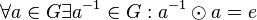  4. Bezüglich \odot existiert zu jedem a aus G ein ("persönliches") inverses Element a^{-1}: \forall a \in G \exist a^{-1} \in G: a^{-1} \odot a = e.

Das Linkseinslement ist auch Rechtseinslement

Die lange Version der Gruppendefinition fordert, dass wenn das Einselement e sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement a multipliziert eben dieses Element a das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird. Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente.
Es gilt der Satz:

Satz 1

Wenn in einer Halbgruppe ein linksseitiges Einselement und zu jedem Element der Halbgruppe ein linksseitiges inverses Element existiert, so sind dieses Linkseinselement und diese Linksinversen gleichzeitig Rechtseinselement und Rechtsinverse.

Beweis von Satz 1

Übungsaufgabe, Hinweise

  1. Beginnen Sie mit Linksinvers=Rechtsinvers
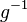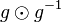
  2. Multiplizieren Sie zunächst das Linksinverse g^{-1} eines beliebigen Elementes g von rechts mit g:g \odot g^{-1}
  3. Ersetzen Sie g durch e \odot g
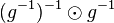  4. Ersetzen Sie e durch das Produkt des Linksinversen vom Linksinversen von g mit dem Linksinversen von g: (g^{-1})^{-1} \odot g^{-1}.
  5. Der Rest ist geschicktes klammern ...
Von „http://geometrie.zum.de/index.php?title=Was_ist_eine_Gruppe%3F_SoSe_2017&oldid=29380“