Lösung von Aufgabe 1.3 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 15: | Zeile 15: | ||
----- | ----- | ||
:Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind. | :Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <math>\odot</math> || e|| a|| b|| c | ||
| + | |- | ||
| + | | e|| Beispiel || Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | a|| Beispiel || Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | b|| Beispiel || Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | c|| Beispiel || Beispiel || Beispiel || Beispiel | ||
| + | |} | ||
'''Definition: "andere Vierergruppe''' | '''Definition: "andere Vierergruppe''' | ||
----- | ----- | ||
:zyklische Viergruppe | :zyklische Viergruppe | ||
Version vom 15. Mai 2017, 10:09 Uhr
Aufgabe 1.3. Algebra SoSe 2017
Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
- Geben Sie für jede der beiden Gruppen zwei Beispiele an.
- Definieren Sie was man unter der Klein'schen Vierergruppe versteht.
- Definieren Sie die andere der beiden Vierergruppen.
Lösungen: zu 1.
- Deckdrehungen des Qudrates: zyklische Gruppe
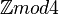: zyklische Gruppe
- Deckabbildungen des Rechtecks: Klein'sche Vierergruppe
- Deckabbildungen der Raute: Klein'sche Vierergruppe
Definition: Klein'sche Vierergruppe
- Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind.
 |
e | a | b | c |
| e | Beispiel | Beispiel | Beispiel | Beispiel |
| a | Beispiel | Beispiel | Beispiel | Beispiel |
| b | Beispiel | Beispiel | Beispiel | Beispiel |
| c | Beispiel | Beispiel | Beispiel | Beispiel |
Definition: "andere Vierergruppe
- zyklische Viergruppe
