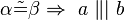Lösung von Aufgabe 4.08 S SoSe 17: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
(→Lösung 1) |
||
| Zeile 6: | Zeile 6: | ||
Hinweis: Führen Sie den Beweis indirekt, indem Sie annehmen, dass <math>a </math> und <math>b</math> nicht parallel sind. Jetzt dürfen Sie den schwachen Außenwinkelsatz (Jeder Außenwinkel ist größer als jeder nichtanliegende Innenwinkel.) anwenden.<br /> | Hinweis: Führen Sie den Beweis indirekt, indem Sie annehmen, dass <math>a </math> und <math>b</math> nicht parallel sind. Jetzt dürfen Sie den schwachen Außenwinkelsatz (Jeder Außenwinkel ist größer als jeder nichtanliegende Innenwinkel.) anwenden.<br /> | ||
==Lösung 1== | ==Lösung 1== | ||
| + | <math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math><br/> | ||
| + | |||
| + | Annahme: | ||
| + | a und b sind nicht parallel, wenn α und β gleich groß sind. | ||
| + | |||
==Lösung 2== | ==Lösung 2== | ||
</div> | </div> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 18. Mai 2017, 16:31 Uhr
Aufgabe 4.08Gegeben seien in der Ebene Lösung 1
Annahme: a und b sind nicht parallel, wenn α und β gleich groß sind. Lösung 2 |
zwei nicht identische Geraden 
und 
. Sowohl 
jeweils in genau einem Punkt geschnitten werden. Beweisen Sie: Wenn bei diesem Schnitt kongruente Stufenwinkel entstehen, dann sind 
