Lösung von Aufgabe 11.8: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung 1) |
(→Lösung 1) |
||
| Zeile 41: | Zeile 41: | ||
--> Beh ist wahr.<br /> | --> Beh ist wahr.<br /> | ||
qed --[[Benutzer:Löwenzahn|Löwenzahn]] 09:36, 3. Jul. 2010 (UTC) | qed --[[Benutzer:Löwenzahn|Löwenzahn]] 09:36, 3. Jul. 2010 (UTC) | ||
| + | |||
| + | Find ich gut, aber dass P denselben Abstand zu A und B hat, haben wir so doch noch nicht bewiesen... | ||
| + | --[[Benutzer:Principella|Principella]] 16:57, 12. Jul. 2010 (UTC) | ||
Version vom 12. Juli 2010, 17:57 Uhr
Beweisen Sie Satz VII.6 b:
Wenn ein Punkt  zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke  gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
Lösung 1
VSS: m ist die Mittelsenkrechte von  ,
, 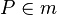
Beh: 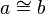
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 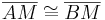
|
(Existenz und Eindeutigkeit Mittelpunkt), (Def. Mittelsenkrechte) |
| (II) | es existiert ein Punkt 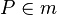
|
(VSS) |
| (III) | 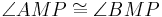
|
(Definition Mittelsenkrechte), (Def. Nebenwinkel), (Supplementaxiom) |
| (IV) | 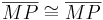
|
(trivial) |
| (V) | 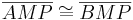
|
(I), (III), (IV), (SWS) |
| (VI) | 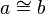 |
(V), (Def Dreieckskongruenz) |
--> Beh ist wahr.
qed --Löwenzahn 09:36, 3. Jul. 2010 (UTC)
Find ich gut, aber dass P denselben Abstand zu A und B hat, haben wir so doch noch nicht bewiesen... --Principella 16:57, 12. Jul. 2010 (UTC)

