Serie 7 SoSe 2017: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.03 SoSe 2017) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.07 SoSe 2017) |
||
| Zeile 39: | Zeile 39: | ||
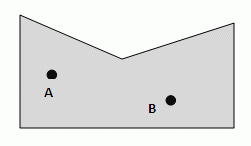
Eine Menge M von Punkten heißt konvex, wenn gilt: <math>\forall A,B \in M: \overline{AB} \subseteq M</math><br\> | Eine Menge M von Punkten heißt konvex, wenn gilt: <math>\forall A,B \in M: \overline{AB} \subseteq M</math><br\> | ||
<br\> | <br\> | ||
| − | + | [[Bild:konvex02.gif|links]] | |
<br\> | <br\> | ||
Student XY argumentiert: "Weil <math>\overline{AB} </math> komplett innerhalb der Punktmenge liegt, ist die obige Figur konvex."<br\> | Student XY argumentiert: "Weil <math>\overline{AB} </math> komplett innerhalb der Punktmenge liegt, ist die obige Figur konvex."<br\> | ||
Version vom 18. Juni 2017, 17:27 Uhr
Inhaltsverzeichnis |
Aufgabe 7.01 SoSe 2017
In einer Übung definierte eine Kommilitonin den Begriff Halbgerade 
wie folgt:
Halbgerade
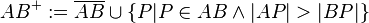
In der Vorlesung wurde wie folgt definiert:
Halbgerade
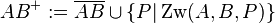Beweisen Sie:
- Definition V
Definition Ü
- Definition Ü Definition V
Aufgabe 7.02 SoSe 2017
Luca aus der 5b erklärt Ihnen: Die Hälfte von einer Ebene ist eine Halbebene. Warum ist diese Begriffserklärung von Luca nicht korrekt?
Aufgabe 7.03 SoSe 2017
Es sei 
eine Ebene und 
ein Punkt außerhalb von .
Definieren Sie Halbraum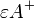 
und Halbraum 
.
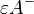Aufgabe 7.04 SoSe 2017
Begründen Sie:
Auf jedem Strahl existiert genau ein Punkt 
, der zu dem Anfangspunkt des Strahls den Abstand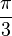 
hat.
Aufgabe 7.05 SoSe 2017
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen? [a)]
-
-
-
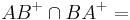
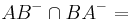
geschnitten mit dem Kreis um 
durch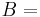 
-
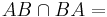
Aufgabe 7.06 SoSe 2017
Beweisen Sie, dass keine Strecke existiert, die zwei Mittelpunkte hat.
Aufgabe 7.07 SoSe 2017
Eine Menge M von Punkten heißt konvex, wenn gilt: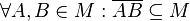 
Student XY argumentiert: "Weil 
komplett innerhalb der Punktmenge liegt, ist die obige Figur konvex."
Wo liegt XY's Denkfehler?
Aufgabe 7.08 SoSe 2017
Definieren Sie den Begriff Halbkreis. (Kreis sei definiert.)
Aufgabe 7.09 SoSe 2017
Definieren Sie den Begriff Dreieck.
Hinweis: Unter einem Dreieck versteht man seine Seiten.
Aufgabe 7.10 SoSe 2017
Definieren Sie den Begriff Viereck.
Hinweis: Vereinigungsmenge der Seiten
