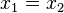Gruppendefinition (Gleichung): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Satz 6) |
||
| Zeile 31: | Zeile 31: | ||
# <math>y \odot a = b</math> | # <math>y \odot a = b</math> | ||
jeweils eindeutig lösbar. | jeweils eindeutig lösbar. | ||
| − | + | ==Beweis von Satz 6== | |
| − | + | Wir führen den Beweis nur für die Gleichung <math>a \odot x= b</math>, für die Gleichung <math>y \odot a = b</math> wird der Beweis analog geführt.<br /> | |
| + | ===Existenzbeweis=== | ||
| + | Wir setzen <math>x=a^{-1}\odot b</math>: <math>a \odot (a^{-1}\odot b) = (a \odot a^{-1}) \odot b = e \odot b = b</math>. | ||
| + | ===Eindeutigkeitsbeweis=== | ||
| + | Es seien <math>x_1</math> und <math>x_2</math> Lösungen der Gleichung <math>a \odot x= b</math>. Damit folgt <math>a \odot x_1 = a \odot x_2</math>. Nach Satz 5 gilt <math>x_1=x_2</math> | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Version vom 25. November 2017, 14:23 Uhr
Eindeutigkeit des EinslementesSatz 3Jede Gruppe hat genau ein Einslement. Beweis von Satz 3Es sei Eindeutigkeit der inversen ElementeSatz 4In jeder Gruppe Beweis von Satz 4Es sei Die triviale Gleichung
KürzbarkeitSatz 5Es sei Beweis von Satz 5Jeweils von rechts bzw. links beide Seiten der Gleichung mit Lösbarkeit der GleichungenSatz 6In jeder Gruppe
jeweils eindeutig lösbar. Beweis von Satz 6Wir führen den Beweis nur für die Gleichung ExistenzbeweisWir setzen EindeutigkeitsbeweisEs seien |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. Nach der Definition des Begriffs Gruppe hat
eine Gruppe. Nach der Definition des Begriffs Gruppe hat 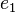 . Es bleibt zu zeigen, dass
. Es bleibt zu zeigen, dass 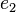 hat. Wir nehmen an es gibt
hat. Wir nehmen an es gibt 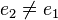 . Nach Satz 2 sind
. Nach Satz 2 sind 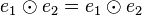 . Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente
. Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente 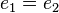 .
.
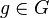 hat genau ein inverses Element.
hat genau ein inverses Element.
 . Nach der Definition des Begriffs Gruppe hat
. Nach der Definition des Begriffs Gruppe hat  in
in  ein Inverses
ein Inverses  bezüglich
bezüglich 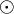 . Wir nehmen an,
. Wir nehmen an, 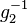 , das natürlich von
, das natürlich von 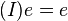 "pumpen" wir zu
"pumpen" wir zu 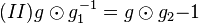 auf.
auf. 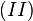 multiplizieren wir auf beiden Seiten von links mit
multiplizieren wir auf beiden Seiten von links mit 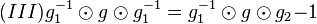 .
.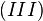 verkürzt sich zu
verkürzt sich zu 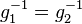 , was ein Widerspruch zu unserer Annahme
, was ein Widerspruch zu unserer Annahme 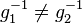 ist.
ist.
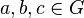 gilt:
gilt: 

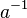 multiplizieren.
multiplizieren.
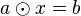 und
und

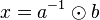 :
: 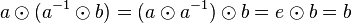 .
.
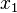 und
und  Lösungen der Gleichung
Lösungen der Gleichung 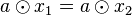 . Nach Satz 5 gilt
. Nach Satz 5 gilt