Übungsaufgabe zur Vorbereitung auf die dritte Sitzung: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 18: | Zeile 18: | ||
# Beweisen Sie: <math> \alpha_1 = 45^\circ , \alpha_3 = 30^\circ , \tan \left( \alpha_2 \right)= \frac{1}{2} \sqrt{2}</math>. | # Beweisen Sie: <math> \alpha_1 = 45^\circ , \alpha_3 = 30^\circ , \tan \left( \alpha_2 \right)= \frac{1}{2} \sqrt{2}</math>. | ||
# Wir betrachten die Drehstreckung <math> \phi = DS_{Z, \beta, k} = \delta_3 \circ \delta_1</math> (erst <math>\ \delta_1</math> dann <math>\ \delta_2</math>). Das Bild <math>\ A^'</math> eines beliebigen Punktes <math>\ A</math> bei <math>\ \phi</math> soll nur mit Zirkel und Lineal konstruiert werden. Geben Sie eine entsprechende Konstruktionsvorschrift an. Begründen Sie die Korrektheit Ihrer Konstruktionsvorschrift. Beachten Sie, dass bei Zirkel und Lineal-Konstruktionen das Lineal keine verfügbare Skala zum Messen hat. | # Wir betrachten die Drehstreckung <math> \phi = DS_{Z, \beta, k} = \delta_3 \circ \delta_1</math> (erst <math>\ \delta_1</math> dann <math>\ \delta_2</math>). Das Bild <math>\ A^'</math> eines beliebigen Punktes <math>\ A</math> bei <math>\ \phi</math> soll nur mit Zirkel und Lineal konstruiert werden. Geben Sie eine entsprechende Konstruktionsvorschrift an. Begründen Sie die Korrektheit Ihrer Konstruktionsvorschrift. Beachten Sie, dass bei Zirkel und Lineal-Konstruktionen das Lineal keine verfügbare Skala zum Messen hat. | ||
| + | # Die Idee der Konstruktion der Punkte <math>\ P^'</math>, <math>\ P^{''}</math>, <math>\ P^{'''}</math> wurde der ''Spirale des Theodorus'' nachempfunden. Wir stellen uns vor, das Verfahren zur Konstruktion weiterer Punkte <math>\ P^{''''}</math>, <math>\ P^{'''''}</math>,… wird analog fortgesetzt (Theodorus wurde nach 17maliger Ausführung der Konstruktion unterbrochen). | ||
Version vom 14. Juli 2010, 14:32 Uhr
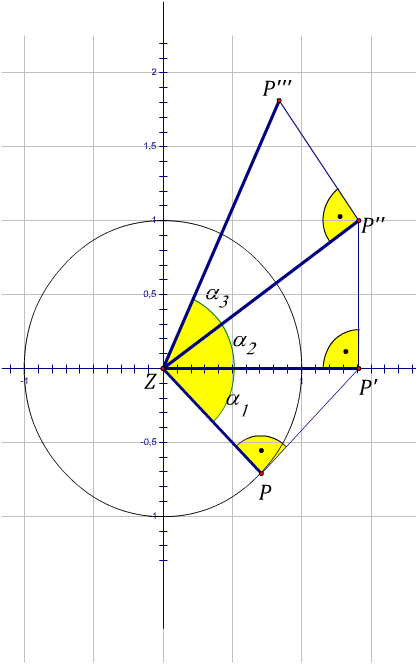
Entsprechend Abbildung 1 wird der Punkt  der Reihe nach durch die Drehstreckungen
der Reihe nach durch die Drehstreckungen
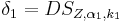 ,
,
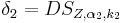 ,
,
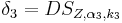 ,
,
auf die Punkte 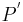 ,
, 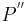 und schließlich auf
und schließlich auf 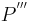 abgebildet.
abgebildet.
Abbildung 1
Es möge 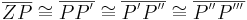 gelten.
gelten.
- Berechnen Sie die Streckfaktoren
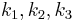 . Begründen Sie Ihre Überlegungen.
. Begründen Sie Ihre Überlegungen.
- Berechnen Sie den Streckfaktor
 der Drehstreckung, die durch die Nacheinanderausführung
der Drehstreckung, die durch die Nacheinanderausführung 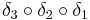 entsteht (erst
entsteht (erst 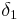 , dann
, dann 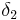 , dann
, dann 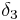 ).
).
- Beweisen Sie:
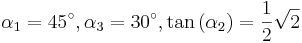 .
.
- Wir betrachten die Drehstreckung
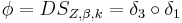 (erst
(erst 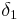 dann
dann 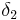 ). Das Bild
). Das Bild 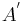 eines beliebigen Punktes
eines beliebigen Punktes  bei
bei  soll nur mit Zirkel und Lineal konstruiert werden. Geben Sie eine entsprechende Konstruktionsvorschrift an. Begründen Sie die Korrektheit Ihrer Konstruktionsvorschrift. Beachten Sie, dass bei Zirkel und Lineal-Konstruktionen das Lineal keine verfügbare Skala zum Messen hat.
soll nur mit Zirkel und Lineal konstruiert werden. Geben Sie eine entsprechende Konstruktionsvorschrift an. Begründen Sie die Korrektheit Ihrer Konstruktionsvorschrift. Beachten Sie, dass bei Zirkel und Lineal-Konstruktionen das Lineal keine verfügbare Skala zum Messen hat.
- Die Idee der Konstruktion der Punkte
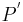 ,
, 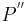 ,
, 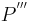 wurde der Spirale des Theodorus nachempfunden. Wir stellen uns vor, das Verfahren zur Konstruktion weiterer Punkte
wurde der Spirale des Theodorus nachempfunden. Wir stellen uns vor, das Verfahren zur Konstruktion weiterer Punkte 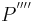 ,
, 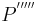 ,… wird analog fortgesetzt (Theodorus wurde nach 17maliger Ausführung der Konstruktion unterbrochen).
,… wird analog fortgesetzt (Theodorus wurde nach 17maliger Ausführung der Konstruktion unterbrochen).