Lösung von Aufgabe 12.6: Unterschied zwischen den Versionen
Nicola (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
== Versuch 1 == | == Versuch 1 == | ||
| − | VSS: Punkt <math> P </math>, Gerade <math> g </math>, <math>P \not \in g </math><br /> | + | VSS: Punkt <math>\ P </math>, Gerade <math>\ g </math>, <math>P \not \in g </math><br /> |
| − | Beh: Gerade <math> h </math>, <math>P \in h</math>, <math>g | + | Beh: Gerade <math>\ h </math>, <math>P \in h</math>, <math>g \| h </math> |
| Zeile 18: | Zeile 18: | ||
|- | |- | ||
! style="background: #FFDDDD;"|(II) | ! style="background: #FFDDDD;"|(II) | ||
| − | | Gerade PQ | + | | Gerade <math>\ PQ</math> |
| (Axiom I.1) | | (Axiom I.1) | ||
|- | |- | ||
! style="background: #FFDDDD;"|(III) | ! style="background: #FFDDDD;"|(III) | ||
| − | | das Maß von <math> | \angle PQR| = \alpha </math> im Punkt <math>P </math> an Gerade <math>PQ </math> in der Halbebene <math>{PQ,R^{+}}</math> abtragen. Es exisitert genau ein <math>{PS^{+}}</math> mit dem Maß <math>|\alpha{'}| | + | | das Maß von <math> | \angle PQR| = \alpha </math> im Punkt <math>\ P </math> an Gerade <math>\ PQ </math> in der Halbebene <math>\ {PQ,R^{+}}</math> abtragen. Es exisitert genau ein <math>\ {PS^{+}}</math> mit dem Maß <math>\ |\alpha{'}| = | \alpha| </math> |
| (Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) | | (Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) | ||
|- | |- | ||
! style="background: #FFDDDD;"|(IV) | ! style="background: #FFDDDD;"|(IV) | ||
| − | | <math>\alpha | + | | <math>\ \alpha' , \alpha </math> sind Stufenwinkel |
| (III), (Def. Stufenwinkel) | | (III), (Def. Stufenwinkel) | ||
|- | |- | ||
! style="background: #FFDDDD;"|(V) | ! style="background: #FFDDDD;"|(V) | ||
| − | | <math>PS </math> = <math> h </math> | + | | <math>\ PS </math> = <math>\ h </math> |
| (Axiom I.1) | | (Axiom I.1) | ||
|- | |- | ||
! style="background: #FFDDDD;"|(V) | ! style="background: #FFDDDD;"|(V) | ||
| − | | <math>g | + | | <math>\ g \| h </math> |
| (Umkehrung Stufenwinkelsatz), (IV), (V) | | (Umkehrung Stufenwinkelsatz), (IV), (V) | ||
|} | |} | ||
| Zeile 43: | Zeile 43: | ||
Zu beweisen sind Existenz und Eindeutigkeit. | Zu beweisen sind Existenz und Eindeutigkeit. | ||
| − | Die Gerade h, die durch den Punkt P geht kann sich zu g auf drei Arten verhalten: | + | <br />Die Gerade h, die durch den Punkt P geht kann sich zu g auf drei Arten verhalten: |
| − | + | ||
| − | + | #Fall: ist identisch => Widerspruch zur Voraussetzung | |
| − | + | #Fall: schneidet h | |
| − | Fall 2 und 3 sind laut Vor. möglich, also existiert auf jeden Fall eine parallele Gerade. | + | #Fall: ist parallel zu h, also schnittpunktfrei |
| − | Die Eindeutigkeit beweise ich indirekt. | + | <br />Fall 2 und 3 sind laut Vor. möglich, also existiert auf jeden Fall eine parallele Gerade. |
| − | Annahme: Es gibt genau zwei Parallelen durch P, die zu g parallel stehen, nämlich h und i, die nicht identisch sind. | + | <br />Die Eindeutigkeit beweise ich indirekt. |
| − | (1) P ist sowohl Element von h, als auch von i. Die Geraden h und i sind damit identisch (Widerspruch Annahme) oder P ist ihr Schnittpunkt. Damit sind i und h aber nicht zueinander parallel (da nicht schnittpunktfrei). Parallelität ist transitiv. Wenn h und i nicht parallel sind, dann gilt entweder h parallel zu g oder i parallel zu g. Damit gibt es wieder nur eine Gerade durch P, die zu g parallel ist und nicht zwei. | + | <br />Annahme: Es gibt genau zwei Parallelen durch P, die zu g parallel stehen, nämlich h und i, die nicht identisch sind. |
| + | <br />(1) P ist sowohl Element von h, als auch von i. Die Geraden h und i sind damit identisch (Widerspruch Annahme) oder P ist ihr Schnittpunkt. Damit sind i und h aber nicht zueinander parallel (da nicht schnittpunktfrei). Parallelität ist transitiv. Wenn h und i nicht parallel sind, dann gilt entweder h parallel zu g oder i parallel zu g. Damit gibt es wieder nur eine Gerade durch P, die zu g parallel ist und nicht zwei. | ||
--[[Benutzer:Nicola|Nicola]] 15:49, 14. Jul. 2010 (UTC) | --[[Benutzer:Nicola|Nicola]] 15:49, 14. Jul. 2010 (UTC) | ||
Version vom 14. Juli 2010, 23:27 Uhr
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Versuch 1
VSS: Punkt  , Gerade
, Gerade  ,
, 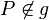
Beh: Gerade  ,
, 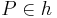 ,
, 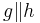
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 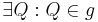 , , 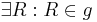
|
(Axiom I.0) |
| (II) | Gerade 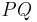
|
(Axiom I.1) |
| (III) | das Maß von 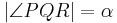 im Punkt im Punkt  an Gerade an Gerade 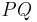 in der Halbebene in der Halbebene 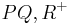 abtragen. Es exisitert genau ein abtragen. Es exisitert genau ein 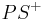 mit dem Maß mit dem Maß 
|
(Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) |
| (IV) | 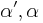 sind Stufenwinkel sind Stufenwinkel
|
(III), (Def. Stufenwinkel) |
| (V) | 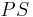 = = 
|
(Axiom I.1) |
| (V) | 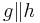
|
(Umkehrung Stufenwinkelsatz), (IV), (V) |
--> Beh ist wahr.
--Löwenzahn 11:07, 14. Jul. 2010 (UTC)
Mal wieder formlos: folgender Vorschlag:
Zu beweisen sind Existenz und Eindeutigkeit.
Die Gerade h, die durch den Punkt P geht kann sich zu g auf drei Arten verhalten:
- Fall: ist identisch => Widerspruch zur Voraussetzung
- Fall: schneidet h
- Fall: ist parallel zu h, also schnittpunktfrei
Fall 2 und 3 sind laut Vor. möglich, also existiert auf jeden Fall eine parallele Gerade.
Die Eindeutigkeit beweise ich indirekt.
Annahme: Es gibt genau zwei Parallelen durch P, die zu g parallel stehen, nämlich h und i, die nicht identisch sind.
(1) P ist sowohl Element von h, als auch von i. Die Geraden h und i sind damit identisch (Widerspruch Annahme) oder P ist ihr Schnittpunkt. Damit sind i und h aber nicht zueinander parallel (da nicht schnittpunktfrei). Parallelität ist transitiv. Wenn h und i nicht parallel sind, dann gilt entweder h parallel zu g oder i parallel zu g. Damit gibt es wieder nur eine Gerade durch P, die zu g parallel ist und nicht zwei.
--Nicola 15:49, 14. Jul. 2010 (UTC)

