Untergruppen, Untergruppenkriterien: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beispiel 2) |
*m.g.* (Diskussion | Beiträge) (→[\Beta, \circ] ist Gruppe) |
||
| Zeile 61: | Zeile 61: | ||
Es seien <math>\alpha</math> und <math>\beta</math> zwei Bewegungen.<br /> | Es seien <math>\alpha</math> und <math>\beta</math> zwei Bewegungen.<br /> | ||
Wir haben zu zeigen, dass <math>\alpha \circ \beta</math> eine Bewegung ist.<br /> | Wir haben zu zeigen, dass <math>\alpha \circ \beta</math> eine Bewegung ist.<br /> | ||
| − | Da die NAF zweier Abbildungen | + | Da die NAF zweier Abbildungen der Ebene auf sich ist tivialerweise wieder eine Abbildung der Ebene auf sich. Wir müssen nur zeigen dass <math>\alpha \circ \beta</math> abstandserhaltend ist:<br /> |
<math> | <math> | ||
\begin{matrix} | \begin{matrix} | ||
| Zeile 68: | Zeile 68: | ||
(3) & \vert PQ \vert= \vert \beta(\alpha(P)) \beta(\alpha(Q)) \vert & (1), (2) | (3) & \vert PQ \vert= \vert \beta(\alpha(P)) \beta(\alpha(Q)) \vert & (1), (2) | ||
\end{matrix} | \end{matrix} | ||
| − | |||
</math> | </math> | ||
| + | ====Assoziativität==== | ||
| + | Die NAF von Abbildungen ist immer assoziativ. | ||
| + | ====Einselement==== | ||
| + | Wir betrachten die Abbildung <math>\operatorname{id}</math>, die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:<br /> | ||
| + | <math>\forall P \in \varepsilon: \operatorname{id}(P)=P</math><math></math><br /> | ||
| + | Damit ist <math>\operatorname{id}</math> eine Abbildung der Ebene auf sich. Wegen <math>\operatorname{id}(A)=A \land \operatorname{id}(B)= B, \forall A,B | ||
| + | \in \varepsilon</math> gilt natürlich auch <math>\vert AB\vert = \vert \operatorname{id}(A) \operatorname{id}(B)\vert</math>. | ||
| + | |||
| + | |||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Version vom 27. Mai 2018, 14:41 Uhr
Beispiele, GegenbeispieleBeispiel 1Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus
Wir wählen aus
Beispiel 2Die Gruppe der BewegungenDie GruppenmitgliederUnter einer Bewegung
|
![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) .
.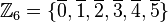




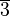
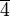
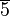
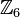 die folgende Teilmenge
die folgende Teilmenge 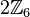 aus:
aus: 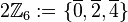
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von
ist eine Gruppe und damit eine Untergruppe von  versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
versteht man eine abstandserhaltende Abbildung der Ebene auf sich: unsere Ebene.
unsere Ebene.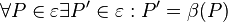
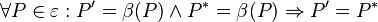
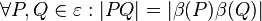
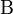 bezeichnen.
bezeichnen.
 .
.
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe
ist Gruppe und
und 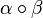 eine Bewegung ist.
eine Bewegung ist.
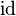 , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:
, die jeden Punkt die Abbildung der ebene auf sich selbst abbildet: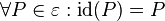
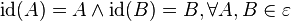 gilt natürlich auch
gilt natürlich auch 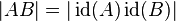 .
.

