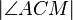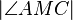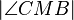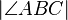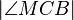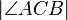Serie 3 SoSe 2018: Unterschied zwischen den Versionen
(→Aufgabe 3.5 SoSe 2018) |
(→Aufgabe 3.6 SoSe 2018) |
||
| Zeile 45: | Zeile 45: | ||
<math>\overline{ABCD}</math> und <math>\overline{EFGH}</math> seien Quadrate. Die einzelnen schraffierten Punktmengen seien das Innere von Viertelkreisen.<br /><br /> | <math>\overline{ABCD}</math> und <math>\overline{EFGH}</math> seien Quadrate. Die einzelnen schraffierten Punktmengen seien das Innere von Viertelkreisen.<br /><br /> | ||
Beweisen Sie: Der prozentuale Anteil der schraffierten Flächen in Bezug auf die Fläche des jeweiligen Quadrats <math>\overline{ABCD}</math> bzw.<math>\overline{EFGH}</math> ist gleich.<br /> | Beweisen Sie: Der prozentuale Anteil der schraffierten Flächen in Bezug auf die Fläche des jeweiligen Quadrats <math>\overline{ABCD}</math> bzw.<math>\overline{EFGH}</math> ist gleich.<br /> | ||
| − | + | [[Datei:Aufgabe 3.6.JPG|thumb|Aufgabe 3.6]] | |
=Aufgabe 3.7 SoSe 2018= | =Aufgabe 3.7 SoSe 2018= | ||
Version vom 9. Juni 2018, 17:54 Uhr
Übungsaufgaben zum 01.05.2018
Inhaltsverzeichnis[Verbergen] |
Aufgabe 3.1 SoSe 2018
Es sei 
ein Dreieck mit den schulüblichen Bezeichnungen. Der Winkel bei 
sei der größte Winkel in diesem Dreieck. Formulieren Sie mit den speziellen Seiten- und Winkelbezeichnungen für dieses Dreieck
(a) den Satz des Pythagoras,
(b) die Umkehrung des Satzes von Pythagoras,
(c) die Kontraposition des Satzes von Pythagoras.
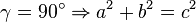
Aufgabe 3.2 SoSe 2018
Es sei ein Dreieck mit schulüblichen Bezeichnungen. Der Innenwinkel 
sei ein Rechter.
Beweisen Sie:
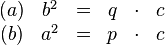
Den Satz des Pythagoras und den Höhensatz für rechtwinklige Dreiecke dürfen Sie als bewiesen voraussetzen.
Aufgabe 3.3 SoSe 2018
Zwischendurch eine Definition:
Ergänzen Sie für die ebene Geometrie:
Definition: (Bild eines Punktes bei einer Spiegelung an einer Geraden)
- Es sei
eine Gerade.
- Der Punkt
wird bei der Spiegelung an auf sich selbst abgebildet, wenn ...
- Ansonsten gilt für und sein Bild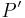
bei der Spiegelung an ...
- Der Punkt
- Es sei
Aufgabe 3.4 SoSe 2018
Wiederholen Sie die Definition von Sinus und Cosinus am Einheitskreis. Beweisen Sie den trigonometrischen Pythagoras.
Aufgabe 3.5 SoSe 2018
Es sei 
ein Kreis mit dem Mittelpunkt 
. Definieren Sie, was man unter einem Durchmesser von versteht.
Aufgabe 3.6 SoSe 2018
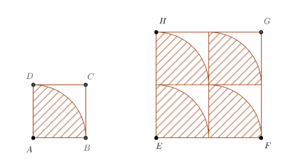
und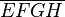 
seien Quadrate. Die einzelnen schraffierten Punktmengen seien das Innere von Viertelkreisen.
Beweisen Sie: Der prozentuale Anteil der schraffierten Flächen in Bezug auf die Fläche des jeweiligen Quadrats bzw.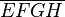 ist gleich.
Aufgabe 3.7 SoSe 2018
Gegeben sei ein Dreieck mit dem Umkreis . Der Mittelpunkt von möge ein Punkt der Strecke 
sein. Der Winkel 
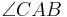habe die Größe 
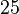°. Berechnen Sie die folgenden Winkelgrößen:
Begründen Sie die Korrektheit Ihrer Berechnungen außschließlich unter Verwendung der folgenden Sätze:
- Innenwinkelsatz für Dreiecke
- Nebenwinkelsatz
- Basiswinkelsatz für gleichschenklige Dreiecke
Aufgabe 3.8 SoSe 2018
Es sei ein Viereck, dessen Diagonalen einander gegenseitig halbieren. Beweisen Sie: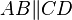 
.
Aufgabe 3.9 SoSe 2018
Die folgende Aussage mögen wahr sein:
(I) Durch zwei verschiedene Punkte geht genau eine Gerade.
Wir betrachten den folgenden Satz:
- Wenn zwei Geraden
und 
nicht identisch sind, dann haben Sie nicht mehr als einen Punkt gemeinsam.
- Wenn zwei Geraden
(a) Beweisen Sie den Satz, indem Sie seine Kontraposition beweisen.
(b) Beweisen Sie den Satz mittels eines Widerspruchsbeweises.
Aufgabe 3.10 SoSe 2018
Wir haben bereits bewiesen, dass aus dem Nebenwinkelsatz der Scheitelwinkesatz folgt. Jetzt machen wir es umgekehrt:
Beweisen Sie, dass aus dem Scheitelwinkelsatz der Nebenwinkelsatz folgt.
