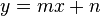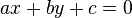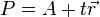Serie 1 Geradengleichungen in der Ebene: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgabe 1= Gegeben seien die Punkte <math>A \left( \frac{1}{2}, \frac{1}{2} \sqrt{3} +2 \right)</math> und <math>B \left(-\sqrt{\frac{4}{3}} , 0 \right)</math>“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
||
| Zeile 1: | Zeile 1: | ||
=Aufgabe 1= | =Aufgabe 1= | ||
| − | Gegeben seien die Punkte <math>A \left( \frac{1}{2}, \frac{1}{2} \sqrt{3} +2 \right)</math> und <math>B \left(-\sqrt{\frac{4}{3}} , 0 \right)</math> | + | Gegeben seien die Punkte <math>A \left( \frac{1}{2}, \frac{1}{2} \sqrt{3} +2 \right)</math> und <math>B \left(-\sqrt{\frac{4}{3}} , 0 \right)</math>. <br /> |
| + | Beschreiben Sie die Gerade <math>AB</math> jeweils durch eine Gleichung der Form | ||
| + | # <math>y=mx+n</math> | ||
| + | # <math>ax+by+c=0</math> | ||
| + | # <math>P=A+t\vec{r}</math> | ||
| + | . | ||
Version vom 2. Mai 2019, 14:41 Uhr
Aufgabe 1
Gegeben seien die Punkte 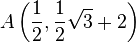 und
und 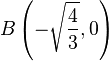 .
.
Beschreiben Sie die Gerade  jeweils durch eine Gleichung der Form
jeweils durch eine Gleichung der Form
.