Lösung von Aufgabe 13.5: Unterschied zwischen den Versionen
(→Versuch 1) |
|||
| Zeile 6: | Zeile 6: | ||
Da es sich bei diesem Satz um eine Äquivalenzrelation handelt ("genau dann") muss die "Hin- und Rückrichtung" bewiesen werden. <br /> | Da es sich bei diesem Satz um eine Äquivalenzrelation handelt ("genau dann") muss die "Hin- und Rückrichtung" bewiesen werden. <br /> | ||
| − | '''1. Hinrichtung:''' "Wenn ein Punkt P zu den Schenkeln von <math> \alpha </math> jeweils denselben Abstand hat, dann gehört er zur Winkelhalbierenden des Winkels <math> \alpha </math>."<br /> | + | '''1. Hinrichtung:''' "Wenn ein Punkt P zu den Schenkeln von <math>\ \alpha </math> jeweils denselben Abstand hat, dann gehört er zur Winkelhalbierenden des Winkels <math>\ \alpha </math>."<br /> |
VSS: <math>\overline{PB} \cong \overline{PA} </math>, <math> \alpha \cong \angle ASB \cong \angle pq </math><br /> | VSS: <math>\overline{PB} \cong \overline{PA} </math>, <math> \alpha \cong \angle ASB \cong \angle pq </math><br /> | ||
| − | Beh: <math> P \in </math> Winkelhalbierende von <math> \alpha </math><br /> | + | Beh: <math> P \in </math> Winkelhalbierende von <math>\ \alpha </math><br /> |
| + | |||
| + | Kommentar --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 16:18, 20. Jul. 2010 (UTC): siehe Diskussion | ||
| + | |||
{| class="wikitable " | {| class="wikitable " | ||
| Zeile 18: | Zeile 21: | ||
|- | |- | ||
! style="background: #FFDDDD;"|(I) | ! style="background: #FFDDDD;"|(I) | ||
| − | | <math> A </math> sei der Lotfußpunkt von P auf den Strahl <math> p </math> und B sei der Lotfußpunkt von P auf den Strahl <math> q </math> | + | | <math>\ A </math> sei der Lotfußpunkt von <math>\ P</math> auf den Strahl <math>\ p </math> und <math> \ B</math> sei der Lotfußpunkt von <math>\ P</math> auf den Strahl <math>\ q </math> |
| (Existenz und Eindeutigkeit Lot) | | (Existenz und Eindeutigkeit Lot) | ||
|- | |- | ||
| Zeile 54: | Zeile 57: | ||
|- | |- | ||
! style="background: #FFDDDD;"|(X) | ! style="background: #FFDDDD;"|(X) | ||
| − | | <math>| \angle ASP| + \angle BSP|= \angle ASB| </math> | + | | <math>|\angle ASP| + |\angle BSP|= |\angle ASB| </math> |
| (IX), (Def. Winkelhalbierende), (Winkeladditionsaxiom) | | (IX), (Def. Winkelhalbierende), (Winkeladditionsaxiom) | ||
|- | |- | ||
! style="background: #FFDDDD;"|(XI) | ! style="background: #FFDDDD;"|(XI) | ||
| − | | <math> {SP^{+}} \cong </math> Winkelhalbierenden von <math> \alpha </math> --> <math> P \in </math> Winkelhalbierende von <math> \alpha </math> | + | | <math> {SP^{+}} \cong </math> Winkelhalbierenden von <math> \alpha \ </math> --> <math>\ P \in </math> Winkelhalbierende von <math>\ \alpha </math> |
| (X) | | (X) | ||
|} | |} | ||
| Zeile 64: | Zeile 67: | ||
| − | '''2. Rückrichtung:''' "Wenn ein Punkt P zur Winkelhalbierenden des Winkels <math> \alpha </math> gehört, dann hat er zu den Schenkeln von <math> \alpha </math> jeweils denselben Abstand."<br /> | + | '''2. Rückrichtung:''' "Wenn ein Punkt P zur Winkelhalbierenden des Winkels <math>\ \alpha </math> gehört, dann hat er zu den Schenkeln von <math>\ \alpha </math> jeweils denselben Abstand."<br /> |
| − | VSS: <math> P \in </math> Winkelhalbierende von <math> \alpha </math> <math> \alpha \cong \angle ASB \cong \angle pq </math> | + | VSS: <math> P \in </math> Winkelhalbierende von <math>\ \alpha </math> und <math> \alpha \cong \angle ASB \cong \angle pq </math> |
<br /> | <br /> | ||
Beh: <math>\overline{PB} \cong \overline{PA} </math><br /> | Beh: <math>\overline{PB} \cong \overline{PA} </math><br /> | ||
| Zeile 77: | Zeile 80: | ||
|- | |- | ||
! style="background: #FFDDDD;"|(I) | ! style="background: #FFDDDD;"|(I) | ||
| − | | <math> P \in </math> Winkelhalbierende von <math> \alpha </math> | + | | <math>\ P \in </math> Winkelhalbierende von <math>\ \alpha </math> |
| (VSS) | | (VSS) | ||
|- | |- | ||
! style="background: #FFDDDD;"|(II) | ! style="background: #FFDDDD;"|(II) | ||
| − | | <math> A </math> sei der Lotfußpunkt von P auf den Strahl <math> p </math> und B sei der Lotfußpunkt von P auf den Strahl <math> q </math> | + | | <math>\ A </math> sei der Lotfußpunkt von <math>\ P</math> auf den Strahl <math>\ p </math> und <math>\ B</math> sei der Lotfußpunkt von <math>\ P</math> auf den Strahl <math>\ q </math> |
| (Existenz und Eindeutigkeit des Lotes) | | (Existenz und Eindeutigkeit des Lotes) | ||
|- | |- | ||
Version vom 20. Juli 2010, 17:18 Uhr
Man beweise: Ein Punkt  gehört genau dann zur Winkelhalbierenden des Winkels
gehört genau dann zur Winkelhalbierenden des Winkels  , wenn er zu den Schenkeln von
, wenn er zu den Schenkeln von  jeweils denselben Abstand hat.
jeweils denselben Abstand hat.
Versuch 1
Da es sich bei diesem Satz um eine Äquivalenzrelation handelt ("genau dann") muss die "Hin- und Rückrichtung" bewiesen werden.
1. Hinrichtung: "Wenn ein Punkt P zu den Schenkeln von  jeweils denselben Abstand hat, dann gehört er zur Winkelhalbierenden des Winkels
jeweils denselben Abstand hat, dann gehört er zur Winkelhalbierenden des Winkels  ."
."
VSS: 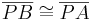 ,
, 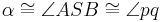
Beh: 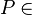 Winkelhalbierende von
Winkelhalbierende von 
Kommentar --Heinzvaneugen 16:18, 20. Jul. 2010 (UTC): siehe Diskussion
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) |  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl  und und  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl 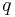
|
(Existenz und Eindeutigkeit Lot) |
| (II) | 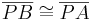
|
(VSS) |
| (III) | 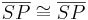
|
(trivial) |
| (IV) | 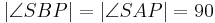
|
(Definition Lot) |
| (V) | 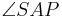 ist größter Winkel im Dreieck ist größter Winkel im Dreieck 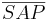
|
(Satz: höchstens ein rechter Winkel im Dreieck), (IV) |
| (VI) | 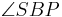 ist größter Winkel im Dreieck ist größter Winkel im Dreieck 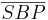
|
(Satz: höchstens ein rechter Winkel im Dreieck), (IV) |
| (VII) | 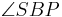 liegt der Seite liegt der Seite  gegenüber gegenüber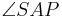 liegt der Seite liegt der Seite  gegenüber gegenüber
|
(Satz: größter Winkel liegt längsten Seite gegenüber),(V), (VI) |
| (VIII) | 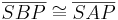
|
(SSW), (VII), (IV), (III), (II) |
| (IX) | 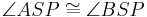
|
(VIII), (Def. Dreieckskongruenz) |
| (X) | 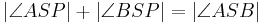
|
(IX), (Def. Winkelhalbierende), (Winkeladditionsaxiom) |
| (XI) | 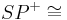 Winkelhalbierenden von Winkelhalbierenden von 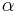 --> --> 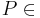 Winkelhalbierende von Winkelhalbierende von 
|
(X) |
--> Beh. wahr qed
2. Rückrichtung: "Wenn ein Punkt P zur Winkelhalbierenden des Winkels  gehört, dann hat er zu den Schenkeln von
gehört, dann hat er zu den Schenkeln von  jeweils denselben Abstand."
jeweils denselben Abstand."
VSS: 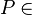 Winkelhalbierende von
Winkelhalbierende von  und
und 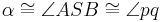
Beh: 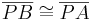
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 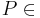 Winkelhalbierende von Winkelhalbierende von 
|
(VSS) |
| (II) |  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl  und und  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl 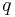
|
(Existenz und Eindeutigkeit des Lotes) |
| (III) | 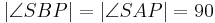
|
(II), (Def. Lot) |
| (IV) | 
|
(Def. Winkelhalbierende) |
| (V) | 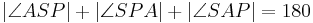
|
(Innenwinkelsumme im Dreieck) |
| (VI) | 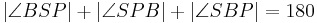
|
(Innenwinkelsumme im Dreieck) |
| (VII) | 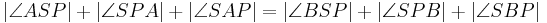
|
(V), (VI), (rechnen mit reellen Zahlen) |
| (VIII) | 
|
(VII), (IV), (rechnen mit reellen Zahlen) |
| (IX) | 
|
(IX), (III), (rechnen mit reellen Zahlen) |
| (X) | 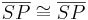
|
(trivial) |
| (XI) | 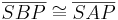
|
(WSW), (X), (IX), (IV) |
| (XII) | 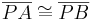
|
(XI), (Def. Dreieckskongruenz) |
-->Beh wahr. qed
Somit ist die Äquivalenz gezeigt --Löwenzahn 11:35, 17. Jul. 2010 (UTC)

