Lösung von Aufg. 7.2P (SoSe 20): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 6: | Zeile 6: | ||
Korrekt! Vielleicht kannst du das in eine mathematische Schreibweise verpacken. --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 11:34, 9. Jun. 2020 (CEST) | Korrekt! Vielleicht kannst du das in eine mathematische Schreibweise verpacken. --[[Benutzer:Tutorin Laura|Tutorin Laura]] ([[Benutzer Diskussion:Tutorin Laura|Diskussion]]) 11:34, 9. Jun. 2020 (CEST) | ||
| − | Es sei das Dreieck ABC. Das Innere des Dreiecks ABC ist: <math>\overline{AB}C^+ \cup \overline{AC}B^+ \cup \overline{BC}A^+</math> | + | Es sei das Dreieck ABC. Das Innere des Dreiecks ABC ist: <math>\overline{AB}C^+ \cup \overline{AC}B^+ \cup \overline{BC}A^+</math> --[[Benutzer:Kohlhoffj|tgksope]] ([[Benutzer Diskussion:Kohlhoffj|Diskussion]]) 12:28, 23. Jul. 2020 (CEST) |
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 23. Juli 2020, 11:28 Uhr
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks 
.
Es sei das Dreieck ABC. Das Innere des Dreiecks ABC ist die Schnittmenge der Halbebenen ABC+, ACB+ und BCA+. --tgksope (Diskussion)
Korrekt! Vielleicht kannst du das in eine mathematische Schreibweise verpacken. --Tutorin Laura (Diskussion) 11:34, 9. Jun. 2020 (CEST)
Es sei das Dreieck ABC. Das Innere des Dreiecks ABC ist: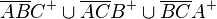 
--tgksope (Diskussion) 12:28, 23. Jul. 2020 (CEST)
