Lösung von Aufg. 7.2P (SoSe 20)

Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks $\overline{ABC}$.

Es sei das Dreieck ABC. Das Innere des Dreiecks ABC ist die Schnittmenge der Halbebenen ABC+, ACB+ und BCA+. --tgksope (Diskussion)

Korrekt! Vielleicht kannst du das in eine mathematische Schreibweise verpacken. --Tutorin Laura (Diskussion) 11:34, 9. Jun. 2020 (CEST)

Es sei das Dreieck ABC. Das Innere des Dreiecks ABC ist: 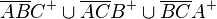$\overline{AB}C^+ \cup \overline{AC}B^+ \cup \overline{BC}A^+$ --tgksope (Diskussion) 12:28, 23. Jul. 2020 (CEST)

Du hast statt der Schnittmenge das Zeichen für die Vereinigungsmenge gesetzt. Wenn du das änderst, dann ist es korrekt.
Du kannst auch schreiben: $I (\overline { ABC }) := ABC^+  \cap  ACB^+  \cap BCA^+$  --Tutorin Laura (Diskussion) 19:09, 23. Jul. 2020 (CEST)