Das Euklidische Parallelenaxiom: Unterschied zwischen den Versionen

Version vom 23. Juli 2010, 21:44 Uhr

Geschichte des Parallelenaxioms

Vater und Sohn Bolyai

Du darfst die Parallelen nicht auf jenem Wege versuchen; ich kenne diesen Weg bis an sein Ende — auch ich habe diese bodenlose Nacht durchmessen, jedes Licht, jede Freude meines Lebens sind in ihr ausgelöscht worden — ich beschwöre Dich bei Gott — laß die Lehre von den Parallelen in Frieden. . . sie kann Dich um all Deine Ruhe, Deine Gesundheit und um Dein ganzes Lebensglück bringen. . . .Wenn ich die Parallelen hätte entdecken können, so wäre ich ein Engel geworden. . . . Es ist unbegreiflich, daß diese unabwendbare Dunkelheit, diese ewige Sonnenfinsternis, dieser Makel der Geometrie zugelassen wurde, diese ewige Wolke an der jungfräulichen Wahrheit.

Farkas Bolyai (in einem Brief an seinen Sohn Janos Bolyai, 1820) ([1], S. 162)

http://de.wikipedia.org/wiki/Farkas_Bolyai
http://de.wikipedia.org/wiki/Janos_Bolyai

Carl Friedrich Gauß

http://de.wikipedia.org/wiki/Carl_Friedrich_Gau%C3%9F

Николай Иванович Лобачевский

http://de.wikipedia.org/wiki/Lobatschewski

Das Euklidische Parallelenaxiom

EP

Zu jedem Punkt außerhalb einer Geraden gibt es höchstens eine Gerade , die durch geht und zu parallel ist.

Sätze über Winkel an geschnittenen Parallelen

Der Stufenwinkelsatz

Satz XII.1: (Stufenwinkelsatz)

Es seien und zwei zueinander parallele Geraden, die durch eine dritte Gerade geschnitten werden. Die bei diesem Schnitt entstehenden Stufenwinkel sind kongruent zueinander.

Ist das ok?--Löwenzahn 16:33, 16. Jul. 2010 (UTC)

Beweis: Lösung von Aufgabe 12.10

Der Wechselwinkelsatz

Satz XII.2: (Wechselwinkelsatz)

Es seien und zwei zueinander parallele Geraden, die durch eine dritte Gerade geschnitten werden. Die bei diesem Schnitt entstehenden Wechselwinkel sind kongruent zueinander.

Die Umkehrung würde doch auch gehen, oder?
Versuch:
Es seien und zwei verschiedene Geraden, durch durch eine weitere Gerade geschnitten werden. Wenn die bei diesem Schnitt entstehenden Wechselwinkel kongruent zueinander sind, so sind die Geraden und parallel zueinander.

Ist das ok?--Löwenzahn 16:33, 16. Jul. 2010 (UTC)

Der Satz über die entgegengesetzt liegenden Winkel an geschnittenen Parallelen

Satz XII.3

Es seien und zwei zueinander parallele Geraden, die durch eine dritte Gerade geschnitten werden. Die bei diesem Schnitt entstehenden entgegengesetzt liegenden Winkel sind kongruent zueinander.

Die Umkehrung würde doch auch gehen, oder?
Versuch 1:
Es seien und zwei verschiedene Geraden, durch durch eine weitere Gerade geschnitten werden. Wenn die bei diesem Schnitt entstehenden entgegengesetzt liegenden Winkel kongruent supplementär zueinander sind, so sind die Geraden und parallel zueinander.

Ist das ok? --Löwenzahn 16:34, 16. Jul. 2010 (UTC)

Sind entgegengesetzt liegende Winkel wirklich kongruent zueinander, überlegen Sie nochmal?! --Schnirch 11:48, 19. Jul. 2010 (UTC)

Oh, supplementär... habe es hoffentlich richtig verbessert.--Löwenzahn 15:55, 20. Jul. 2010 (UTC)
Dann muss es aber im Satz XII.3 ebenfalls supplementär heißen, oder? --Barbarossa 20:44, 23. Jul. 2010 (UTC)

Versuch 2:
Es seien und zwei verschiedene Geraden, durch durch eine weitere Gerade geschnitten werden. Wenn die bei diesem Schnitt entstehenden entgegengesetzt liegenden Winkel supplementär sind, die Größen sich also auf 180 summieren, so sind die Geraden und parallel zueinander.

Begründung: Der jeweilige Nebenwinkel des einen Winkels ist entweder Stufenwinkel oder Wechselwinkel bezüglich des anderen Winkels, die wiederum kongruent zueinander sind.
Winkel 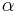(Scheitelpunkt ist Schnittpunkt von und )
Winkel 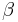(Scheitelpunkt ist Schnittpunkt von und )
Winkel 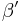(Nebenwinkel zu 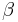) ist Stufenwinkel (analog: Wechselwinkel) zu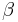
Wenn 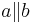, dann ist 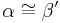und da (wg. Supplementaxiom) gilt, dass 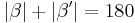, gilt auch .

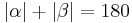Überlegung --Löwenzahn 16:02, 20. Jul. 2010 (UTC): Ist das der Beweis für die Implikation oder die Umkehrung des Satzes zu entgegengesetzt liegende Winkel???