Lösung von Aufgabe 10.5P (WS 23 24): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{…“) |
End007 (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=S_a\circ S_b(P) </math>.<br /> | Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=S_a\circ S_b(P) </math>.<br /> | ||
| − | + | [[Datei:Aufg. 10.5 End007.jpeg|thumb|Vorschlag]]--[[Benutzer:End007|End007]] ([[Benutzer Diskussion:End007|Diskussion]]) 12:15, 13. Jan. 2024 (CET) | |
| + | Kann man das so machen? Es ist irgendwie so offensichtlich, dass es mir schwer fällt die richtigen und wichtigen Beweis-Schritte zu formulieren. | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 13. Januar 2024, 12:15 Uhr
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 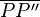 , mit
, mit 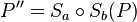 .
.
Kann man das so machen? Es ist irgendwie so offensichtlich, dass es mir schwer fällt die richtigen und wichtigen Beweis-Schritte zu formulieren.


