Lösung von Aufgabe 10.5P (WS 23 24)

Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 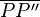$\overline{PP''}$, mit $P''=S_a\circ S_b(P)$.

Vorschlag

--End007 (Diskussion) 12:15, 13. Jan. 2024 (CET)

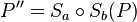Kann man das so machen? Es ist irgendwie so offensichtlich, dass es mir schwer fällt die richtigen und wichtigen Beweis-Schritte zu formulieren.

Hi der Beweis an sich ist richtig geführt :). Nur leider beweist er nur, dass der Abstand von P und P`` zu S der gleiche ist. Du müsstest noch beweisen, dass die beiden Punkte auf einer Geraden liegen, um dann zu schlussfolgern, dass S der Mittelpunkt von P und P´´ ist.

Versuche den Beweis noch einmal zu Starten und mit dem Satz zu arbeiten, dass man die Spiegelgeraden bei Drehungen beliebig drehen kann, solange der Winkel und der Schnittpunkt gleich bleiben. :)--Matze2000 (Diskussion) 15:10, 13. Jan. 2024 (CET)

Vorschlag Capricorn 10.5

--Capricorn (Diskussion) 20:01, 13. Jan. 2024 (CET)

Hi Capricorn. Auch bei dir gilt: die Behauptung "|PS|=|P``S|" ist nicht ausreichend. Wir wollen beweisen, dass S Mittelpunkt der Strecke PP`` ist. Hierfür müssen wir zusätzlich zu dem gleich großen Abstand auch noch zeigen, dass P und P´´ auf einer Geraden durch S liegen.--Matze2000 (Diskussion) 16:51, 14. Jan. 2024 (CET)