Geradenspiegelungen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Übungsaufgabe) |
(→Definition 2.1: (Spiegelung an der Geraden \ g)) |
||
| Zeile 32: | Zeile 32: | ||
=====Definition 2.1: (Spiegelung an der Geraden <math>\ g</math>)===== | =====Definition 2.1: (Spiegelung an der Geraden <math>\ g</math>)===== | ||
::Es sei <math>\ g</math> eine Gerade. Unter der Geradenspiegelung <math>\ S_g</math> versteht man eine .... | ::Es sei <math>\ g</math> eine Gerade. Unter der Geradenspiegelung <math>\ S_g</math> versteht man eine .... | ||
| + | |||
| + | ::Es sei <math>\ g</math> eine Gerade und P ein Punkkt der Ebene. Unter der Geradenspiegelung <math>\ S_g</math> versteht man eine Abbildung der Ebene auf sich: | ||
| + | (1) Für den Fall dass P <math>\in</math> <math>\ g</math>: P = P' | ||
| + | |||
| + | (2) Für den fall dass P <math>\notin</math> <math>\ g</math>: Die Gerade <math>\ g</math> ist Mittelsenkrechte der Strecke zwischen dem Punkt P und seinem Bildpunkt P' | ||
==Die Geradenspiegelung als spezielle Bewegung== | ==Die Geradenspiegelung als spezielle Bewegung== | ||
=====Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)===== | =====Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)===== | ||
::Jede Geradenspiegelung <math>\ S_g</math> ist eine abstandserhaltende Abbildung. | ::Jede Geradenspiegelung <math>\ S_g</math> ist eine abstandserhaltende Abbildung. | ||
Version vom 27. Oktober 2010, 10:03 Uhr
Inhaltsverzeichnis |
Konstruktion des Bildes eines Punktes 
bei einer Spiegelung an der Geraden 
Übungsaufgabe
Es sei ein Punkt der Ebene der nicht zur Geraden dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von bei der Spiegelung an . Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. | Beschreibung 1. | Begründung 1. |
| 2. | Beschreibung 2. | Begründung 2. |
| 3. | Beschreibung 3. | Begründung 3. |
Definition des Begriffs
Definition 2.1: (Spiegelung an der Geraden )
- Es sei eine Gerade. Unter der Geradenspiegelung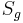
versteht man eine ....
- Es sei
- Es sei eine Gerade und P ein Punkkt der Ebene. Unter der Geradenspiegelung 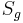versteht man eine Abbildung der Ebene auf sich:
- Es sei
(1) Für den Fall dass P 
: P = P'
(2) Für den fall dass P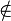 
: Die Gerade ist Mittelsenkrechte der Strecke zwischen dem Punkt P und seinem Bildpunkt P'
Die Geradenspiegelung als spezielle Bewegung
Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)
- Jede Geradenspiegelung 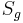ist eine abstandserhaltende Abbildung.
- Jede Geradenspiegelung
