Lösung von Aufgabe 5.7: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 5: | Zeile 5: | ||
* Die Figuren stehen in der Relation konvex zu sein<br /> | * Die Figuren stehen in der Relation konvex zu sein<br /> | ||
* Die Figuren stehen in der Relation n Eck mit n kleiner 5 zu sein--[[Benutzer:Engel82|Engel82]] 00:27, 11. Nov. 2010 (UTC) | * Die Figuren stehen in der Relation n Eck mit n kleiner 5 zu sein--[[Benutzer:Engel82|Engel82]] 00:27, 11. Nov. 2010 (UTC) | ||
| + | |||
| + | |||
| + | Weiter Relationen könnten sein: | ||
| + | * Die Fieguren stehen in der Relation haben die gleiche Farbe<br /> | ||
| + | * Die Fieguren stehen in der Relation sind im Uhrzeigersinn Beschriftet<br /> | ||
| + | * Die Fieguren stehen in der Relation haben mindestens drei Eckpunkte<br /> | ||
| + | * Die Fieguren stehen in der Relation liegen in der selben Ebene | ||
| + | |||
| + | --[[Benutzer:Rakorium|Rakorium]] 10:01, 14. Nov. 2010 (UTC) | ||
Version vom 14. November 2010, 11:01 Uhr
Es sei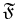 
die Menge der Figuren der Ebene. Auf 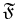sei eine Äquivalenzrelation 
definiert. möge 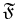derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen:
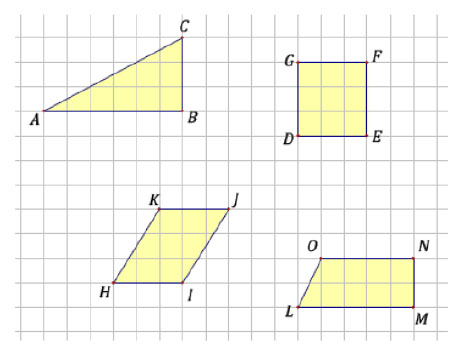
Geben Sie mögliche Interpretationen der Relation an.
- Die Figuren stehen in der Relation flächengleich
- Die Figuren stehen in der Relation konvex zu sein
- Die Figuren stehen in der Relation n Eck mit n kleiner 5 zu sein--Engel82 00:27, 11. Nov. 2010 (UTC)
Weiter Relationen könnten sein:
- Die Fieguren stehen in der Relation haben die gleiche Farbe
- Die Fieguren stehen in der Relation sind im Uhrzeigersinn Beschriftet
- Die Fieguren stehen in der Relation haben mindestens drei Eckpunkte
- Die Fieguren stehen in der Relation liegen in der selben Ebene
--Rakorium 10:01, 14. Nov. 2010 (UTC)
