Lösung von Aufg. 6.7: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: Es seien <math>\ P_1, P_2, P_3, ..., P_n \ n</math> verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es...) |
Hasekm (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Es seien <math>\ P_1, P_2, P_3, ..., P_n \ n</math> verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser <math>n</math> Punkte gehen? | Es seien <math>\ P_1, P_2, P_3, ..., P_n \ n</math> verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser <math>n</math> Punkte gehen? | ||
Hinweis: Es gibt eine Problemlösestrategie: ''Führe einen komplizierten Fall auf einen einfacheren Fall zurück''. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe. | Hinweis: Es gibt eine Problemlösestrategie: ''Führe einen komplizierten Fall auf einen einfacheren Fall zurück''. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe. | ||
| + | |||
| + | Also es gibt genau 6 Geraden, diese bilden zusammen einen Tetraeder.--[[Benutzer:Hasekm|Hasekm]] 15:53, 17. Nov. 2010 (UTC)<br /> | ||
Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. | Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. | ||
Version vom 17. November 2010, 16:53 Uhr
Es seien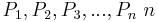 
verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser 
Punkte gehen?
Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.
Also es gibt genau 6 Geraden, diese bilden zusammen einen Tetraeder.--Hasekm 15:53, 17. Nov. 2010 (UTC)
Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. Formulieren Sie obige Aufgabe für Schüler dieser Schulstufe.
