Lösung von Aufg. 6.7

Es seien 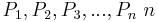$\ P_1, P_2, P_3, ..., P_n \ n$ verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser $n$ Punkte gehen? Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.

Also es gibt genau 6 Geraden, diese bilden zusammen einen Tetraeder.--Hasekm 15:53, 17. Nov. 2010 (UTC)

• Erklärung bitte :)

Meiner meinung nach gibt es genau 6 Geraden für n=4. Aber wir wollen wissen wieviel Geraden es für n viele Punkte gibt. Ich habe erstmal eine Tabelle gemacht

n Geraden
1 0
2 1
3 3
4 6
5 10
6 15

jetzt erkennt man, dass es eine Folge ist, Formel a_n=a_n-1+ (n-1) und a₁=0 Ich bin mir nicht 100%ig sicher, da ich das letzte Mal zu Schulzeiten mit dieser Thematik zu tun hatte, aber es macht so irgendwie sinn ;)--Kaam11 18:50, 30. Nov. 2010 (UTC)

ja, sehr schön, genau so ist es gemeint! Sie haben hier eine so genannte Rekursivformel angegeben.
Sie könnten $\ a_n$ auch folgendermaßen angeben: $\ a_n = \frac{n\cdot \left (n-1 \right)}{2}$ und damit $\ a_n$ bei gegebenen n sofort berechnen.
Hinter der Folge verbergen sich die so genannten Dreieckszahlen.
Auf [dieser Internetseite] finden Sie viele (Schul)Beispiele und Hintergründe zu den Dreieckszahlen.--Schnirch 13:32, 9. Dez. 2010 (UTC) 

Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. Formulieren Sie obige Aufgabe für Schüler dieser Schulstufe.

Beispielsweise könnte man nach der Anzahl der Seiten und Diagonalen von Vielecken fragen,
damit wäre die Nichtkollinearität aller Eckpunkte garantiert.--Schnirch 13:32, 9. Dez. 2010 (UTC)