Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz (WS10/11: Unterschied zwischen den Versionen
TimoRR (Diskussion | Beiträge) (→Idee des Beweises eines Spezialfalls) |
(→Satz XIX.2:(Der Peripheriewinkelsatz)) |
||
| Zeile 48: | Zeile 48: | ||
=== Satz XIX.2:(Der Peripheriewinkelsatz) === | === Satz XIX.2:(Der Peripheriewinkelsatz) === | ||
ergänzen Sie: | ergänzen Sie: | ||
| − | Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--[[Benutzer:Engel82|Engel82]] 13:23, 30. Jan. 2011 (UTC) | + | Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--[[Benutzer:Engel82|Engel82]] 13:23, 30. Jan. 2011 (UTC)<br /> |
| + | <br /> | ||
| + | Im Hinblick darauf, dass wir den Zentri-Peripheriewinkelsatz bereits bewiesen haben, ist dann diese Beweisführung ohne das Sehnenviereck möglich? | ||
| + | <br /> | ||
| + | [[Bild:Scannen0001.jpg|600px]]<br />--[[Benutzer:-mystery-|-mystery-]] 20:51, 6. Feb. 2011 (UTC) | ||
[[Kategorie:Einführung_Geometrie]] | [[Kategorie:Einführung_Geometrie]] | ||
Aktuelle Version vom 6. Februar 2011, 21:51 Uhr
Inhaltsverzeichnis |
Definition XIX.1 (Peripheriewinkel)
Der Winkel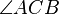 
im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:
Gegeben sei ein Kreis k und die Punkte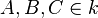 
.
Ein Peripheriewinkel ist ein Winkel, dessen Scheitel in C liegt und dessen Schenkel durch A und B verlaufen.--Engel82 13:17, 30. Jan. 2011 (UTC)
Ein Peripheriewinkel ist ein Winkel, dessen Scheitelpunkt Element eines Kreises ist und dessen Schenkel den Kreis in jeweils einem Punkt schneiden.--TimoRR 12:57, 5. Feb. 2011 (UTC)
Definition XIX.2 (Zentriwinkel)
Der Winkel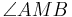 
im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:
Gegeben sei ein Kreis k, M der Mittelpunkt von k und die Punkte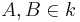 
.
Ein Zentriwinkel ist ein Winkel, dessen Scheitel in M liegt und dessen Schenkel durch A und B verlaufen.--Engel82 13:20, 30. Jan. 2011 (UTC)
Ein Zentriwinkel ist ein Winkel, dessen Scheitelpunkt der Mittelpunkt eines Kreises ist und dessen Schenkel den Kreis in jeweils einem Punkt schneiden.--TimoRR 12:57, 5. Feb. 2011 (UTC)
Idee des Beweises eines Spezialfalls
Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?
verschriftlichte Beweisführung: (Vorschlag)
(1) Durchmesser einzeichnen
(2) es entstehen zwei gleichschenklige Dreiecke wg. (1)
(3) die grünen und roten Winkel sind jeweils kongruent wg. Basiswinkelsatz, (2)
(4) blauer Winkel ist so groß wie zwei grüne Basiswinkel wg. starkem Außenwinkelsatz, (3)
(5) gelber Winkel ist so groß wie zwei rote Basiswinkel wg. starkem Außenwinkelsatz, (3)
(6) Nebenwinkel von blau ist 180 - blau wg. Supplementaxiom
(7) Nebenwinkel von gelb ist 180 - gelb wg. Supplementaxiom
(8) Nebenwinkel von blau ist 180 - 2 grün wg. Innenwinkelsumme im Dreieck, (3)
(9) Nebenwinkel von gelb ist 180 - 2 rot wg. Innenwinkelsumme im Dreieck, (3)
(10)roter + grüner Winkel = Hälfte von blauer + gelber Winkel wg. (8)und(9) einsetzen in (6) und (7) und Rechnen in R
--TimoRR 13:34, 5. Feb. 2011 (UTC)
Der Zentri-Peripheriewinkelsatz
ergänzen Sie: Jeder Peripheriewinkel ist halb so groß wie sein zugehöriger Zentriwinkel.--Engel82 13:22, 30. Jan. 2011 (UTC)
Satz XIX.1:(Der Zentri-Peripheriewinkelsatz)
Der Peripheriewinkelsatz
Satz XIX.2:(Der Peripheriewinkelsatz)
ergänzen Sie:
Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--Engel82 13:23, 30. Jan. 2011 (UTC)
Im Hinblick darauf, dass wir den Zentri-Peripheriewinkelsatz bereits bewiesen haben, ist dann diese Beweisführung ohne das Sehnenviereck möglich?
---mystery- 20:51, 6. Feb. 2011 (UTC)
