Äquivalenzrelationen und Klasseneinteilungen SoSe 11: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (→Definition des Begriffs Klasseneinteilung) |
(→Definition des Begriffs Klasseneinteilung) |
||
| Zeile 72: | Zeile 72: | ||
:# notwendige Bedingung 3: Die Menge K muss echte Teilmenge von M sein, ansonsten wäre K = M und somit keine Klasseneinteilung <br /> | :# notwendige Bedingung 3: Die Menge K muss echte Teilmenge von M sein, ansonsten wäre K = M und somit keine Klasseneinteilung <br /> | ||
--[[Benutzer:HecklF|HecklF]] 21:47, 25. Apr. 2011 (CEST) | --[[Benutzer:HecklF|HecklF]] 21:47, 25. Apr. 2011 (CEST) | ||
| + | <br /> | ||
| + | <span style="color:#000080">mh, weitere Vorschläge, Änderungen...</span>--[[Benutzer:Tutorin Anne|Tutorin Anne]] 21:55, 25. Apr. 2011 (CEST) | ||
== Relationen == | == Relationen == | ||
Version vom 25. April 2011, 20:55 Uhr
Inhaltsverzeichnis |
Ziel der Ausführungen bzw. der Veranstaltung
Es gibt grundlegende Begriffe, die man im Mathematikunterricht und auch im alltäglichen Sprachgebrauch ständig verwendet, ohne sich bis ins letzte Detail Gedanken über den Begriff selbst zu machen. Mitunter braucht man es dann doch genauer und es stellen sich Fragen, die gar nicht so einfach zu beantworten sind:
- Was ist eigentlich eine natürliche Zahl?
- Was ist ein Bruch, was ist eine Bruchzahl, was ist eine gebrochene Zahl und ist das eigentlich alles dasselbe?
- Was ist eine Richtung?
- Was ist der Richtungssinn?
- Meint 3. und 4. dasselbe?
- Was ist ein Pfeil und was sind Pfeilklassen?
Man kann eine ganze Zeit lang Mathematik betreiben, ohne obige Fragen explizit zu beantworten:
- Natürliche Zahlen kennt doch jedes Kind, es sind die Zahlen 1, 2, 3, 4, 5 usw., sie sind offenbar gottgegeben.
- Was interessiert es mich, ob es Bruch, gebrochene Zahl oder Bruchzahl heißt, wenn ich etwa
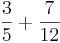 rechnen soll, dann rechne ich halt
rechnen soll, dann rechne ich halt 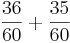 und erhalte
und erhalte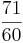 .
.
- 3. bis 6.
 |
Was interessiert es mich, ob es Pfeil oder Pfeilklasse heißt, wenn ich etwa 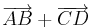 bestimmen soll, dann rechne ich halt bestimmen soll, dann rechne ich halt 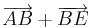 und erhalte und erhalte 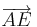
|
Irgendwie bleibt bei näherer Betrachtung der Dinge jedoch ein wenig Unsicherheit, die, je mehr man darüber nachdenkt, immer stärker wird:
Wir haben nicht wirklich die Brüche  und
und 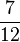 addiert, sondern die Brüche
addiert, sondern die Brüche 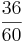 und
und 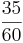 . Irgendwie ist das sicherlich dasselbe, irgendwie aber auch nicht:
. Irgendwie ist das sicherlich dasselbe, irgendwie aber auch nicht:  einer Pizza sind wunderschöne Stücke (Schließlich hat m.g. 10 Jahre das Rezept für seinen Teig optimiert.).
einer Pizza sind wunderschöne Stücke (Schließlich hat m.g. 10 Jahre das Rezept für seinen Teig optimiert.). 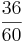 derselben Pizza ist Matsch und nicht wirklich genießbar (eventuell noch für zahnlose Hunde).
derselben Pizza ist Matsch und nicht wirklich genießbar (eventuell noch für zahnlose Hunde).
Irgendwie passt es schon, dass wir anstelle von 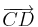
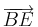 zu
zu 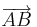 addiert haben. Bei näherer Betrachtung ist der Pfeil
addiert haben. Bei näherer Betrachtung ist der Pfeil 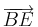 aber auch ein von
aber auch ein von 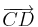 verschiedener Pfeil unserer Ebene.
verschiedener Pfeil unserer Ebene.
Dieses Irgendwie und passt schon sollten wir präzieren. Zentraler Punkt dieser Präzisierung sind die Begriffe Äquivalenzrelation und Klasseneinteilung.
Klasseneinteilungen
Beispiele und Gegenbeispiele
Kleine Bemerkung aus didaktischer Sicht zur Erarbeitung des Begriffs Klasseneinteilung
Die Ausbildung von Lehrern an einer Hochschule oder Universität läuft häufig Gefahr, sich selbst ad absurdum zu führen. Auf der einen Seite fordert man vom zukünftigen Lehrer, dass dieser sich im Praktikum seines didaktischen Know-How's bedienen möge, während man in den eigenen Lehrveranstaltungen den didaktischen Aspekt stark vernachlässigt. Nun wird es rein aus Zeitgründen nicht immer möglich sein, sich in einer Hoschschullehrveranstaltung der Methoden eines Unterricht allgeinbildender Schulen zu bedienen, zumindest exemplarisch sollte es jedoch möglich sein, den stark dozierenden Stil der Hochschullehrveranstaltung zu durchbrechen. Hier und jetzt wollen wir dieses tun: Der Begriff der Klasseneinteilung soll induktiv erarbeitet werden. Hierzu werden wir verschiedene Beispiele und prägnante Gegenbeispiele bezüglich des Begriffes der Klasseneinteilung untersuchen um dann die Idee des Begriffs Klasseneinteilung herauszuarbeiten.
Ein Beispiel für eine Klasseneinteilung
Die übliche morgendliche Hektik an der „Maier-Vorwiesener“ Grund- und Hauptschule: Frau Schulze-Mackenroth zog es für heute vor, ihr Burnout-Syndrom mit Tannenzäpfle und Ouzo zu pflegen, weshalb sie sich kurz vor knapp bei Rektor Pollenwein telefonisch krank gemeldet hat. In ihrer Grundschulklasse geht es derweilen drunter und drüber. Xulio-Dävid hat seine überforderte, allein erziehende Mutter ausgetrickst und das Methylphenidat nicht genommen. Jetzt lässt er seine ADHS hemmungslos an seinen Klassenkameraden aus.
Zu Hause bei Lehrer Steiner gab es ein weiteres mal Stress wegen der jungen blonden Referendarin, die Steiner betreut. Er flüchtet deshalb und kommt eine Stunde früher. Erleichtert sieht ihn Rektor Gendarm beim Anmarsch auf die Schule. Aus dem Rektoratsfenster ruft er Steiner zu: „Du musst ganz schnell in die Klasse von Xulio-Dävid. Es brennt mal wieder!“
Damit ist eindeutig geklärt, in welche Klasse Herr Steiner gehen muss. Rein formal hätte Rektor Gendarm natürlich auch die Namen von anderen Schülern nennen können, die mit Xulio-Dävid in dieselbe Klasse gehen. An der klassischen Grund- und Hauptschule geht jeder Schüler in genau eine Klasse. Ihre Klassen sind ein Beispiel dafür, was der Mathematiker unter einer Klasseneinteilung versteht.
Ein Gegenbeispiel für den Begriff der Klasseneinteilung
10 Jahre ist Sportsfreund Holzkugel nun Vorsitzender des örtlichen Kegelvereins. Es waren bewegte 10 Jahre. Vor 5 Jahren gelang ihm das, woran schon viele Vorsitzende des Vereins scheiterten: Die Öffnung des Vereins für den Bowlingsport. Die Gegner des Bowling verwiesen immer wieder auf den Namen des Vereins: "Alle Neune Wilhelmsfeld". Schließlich konnte man sich aber doch auf eine Umbennung in "Gut Holz Wilhelmsfeld" einigen, was die Gründung der Sektion Bowling ermöglichte. Heute gehört  aller Mitglieder von "Gut Holz Wilhelmsfeld" sowohl der Sektion Kegeln als auch der Sektion Bowling an. Die beiden Sektionen bilden damit keine Klasseneinteilung des Vereins "Gut Holz Wilhelmsfeld".
aller Mitglieder von "Gut Holz Wilhelmsfeld" sowohl der Sektion Kegeln als auch der Sektion Bowling an. Die beiden Sektionen bilden damit keine Klasseneinteilung des Vereins "Gut Holz Wilhelmsfeld".
Identifizieren von Klasseneinteilungen
Definition des Begriffs Klasseneinteilung
Definition: (Klasseneinteilung eine Menge)
- Es sei
 eine Menge und
eine Menge und 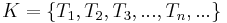 eine Menge von Teilmengen von
eine Menge von Teilmengen von  .
.
 ist eine Klasseneinteilung von
ist eine Klasseneinteilung von  , wenn
, wenn
- Es sei
- notwendige Bedingung 1: Jedes a Element M ist nur in einer Teilmenge von K enthalten (ich weiß leider nicht wo die ganzen kleinen math. Zeichen wie "Element" oder so sind)
- notwendige Bedingung 2: Wieder mit Worten: Die Mächtigkeit jeder Teilmenge T_a Element K ist größer null
- notwendige Bedingung 3: Die Menge K muss echte Teilmenge von M sein, ansonsten wäre K = M und somit keine Klasseneinteilung
--HecklF 21:47, 25. Apr. 2011 (CEST)
mh, weitere Vorschläge, Änderungen...--Tutorin Anne 21:55, 25. Apr. 2011 (CEST)
Relationen
Beispiele
Halt dich senkrecht
Im Schulpraktikum war der Begriff der Senkrechten zu behandeln. Der Praktikant hatte ein Bild der Schweizer Nationalflagge auf eine Folie gedruckt und fragte die Schüler, welche Linien Senkrechte wären. Bei den Schülern stellte sich nach den ersten Antworten leichte Unsicherheit ein.
Der Grund für diese Unsicherheit: Die Frage des Praktikanten war völlig unsinnig. Eine Antwort wie Gerade  steht senkrecht ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von
steht senkrecht ist lediglich eine Aussageform, der kein Wahrheitswert zuzuordnen ist. Erst wenn man die Lage von  bezüglich einer anderen Geraden
bezüglich einer anderen Geraden  (Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass
(Ebene, Strahl, Strecke) betrachtet, ist es sinnvoll davon zu sprechen, dass  eine Senkrechte ist.
eine Senkrechte ist.
Die Relation Gerade  steht senkrecht auf Gerade
steht senkrecht auf Gerade  ist zweistellig.
ist zweistellig.
Eine klassische Dreiecksbeziehung
Tom ist der Liebhaber von Gabi. Zu der Ehre der Liebhabereigenschaft kommt er durch die Existenz von Frank, dem Ehemann von Gabi. Tom, Gabi und Frank stehen in einer dreistelligen Relation zueinander, der klassischen Dreiecksbeziehung.
Wir könnten diese Relation auch so formulieren: Gabi steht zwischen zwei Männern.
Beispiel 3
Trauen Sie sich: Präsentieren Sie hier ein eigenes Beispiel.
Beispiel 4
Trauen Sie sich: Präsentieren Sie hier ein eigenes Beispiel.
Ein Quiz zwischendurch
Die Idee der Relation aus abstrakter Sicht
Jeder mit Jeder?
Von Anfang an war Kommissar Schätzerle dieses Dorf, dass man weder dem Ländle noch dem Nachbarn Bayern so recht zuordnen kann, nicht ganz geheuer gewesen.
Ist nun der schöne Anton der Vater von der Lisa oder doch Stavros, der Grieche, der irgendwann im Dorf auftauchte und seitdem bei der feschen Wirtin wohnt. Wer ist eigentlich der Vater vom Klaus, den man hier immer noch politisch unkorrekt den Dorfdeppen nennt. Und was ist mit Dorothea, deren Zeugung mit Sicherheit nicht die unbefleckte Empfängnis war, alle im Dorf aber so tun, als wenn es so gewesen wäre.
Eins wurde Schätzerle immer klarer: Er konnte den aktuellen Fall nur lösen, indem er alle Vaterschaften des Ortes gnadenlos aufklärte. An die DNS aller in Frage kommender Männer heranzukommen war leicht. Ein abendlicher Besuch bei der feschen Wirtin reichte aus. Schwieriger war es bei den Kindern. Um das Gerichtsverfahren nicht zu gefährden, sei dem Chronisten diesbezügliches Stillschweigen gestattet. Wie auch immer, irgendwann hatte sich Schätzerle auch die noch fehlende DNS von Maria besorgt und schickte alles den Kollegen in Stuttgart zum Zwecke des DNA-Abgleichs.
Mit der Bitte um Kennzeichnung jeweiliger Vaterschaften durch ein Ausrufezeichen schickte er die folgende tabellarische Übersicht mit:
| der schöne Anton | Stavros, der Grieche | der Pfarrer | der Gärtner | |
|---|---|---|---|---|
| Lisa | ? | ? | ? | ? |
| Klaus | ? | ? | ? | ? |
| Dorothea | ? | ? | ? | ? |
| Maria | ? | ? | ? | ? |
| Karl - Theodor | ? | ? | ? | ? |
| Hans | ? | ? | ? | ? |
Das LKA Stuttgart schickte die Tabelle in folgender Form zurück:
| der schöne Anton | Stavros, der Grieche | der Pfarrer | der Gärtner | |
|---|---|---|---|---|
| Lisa | ? | ? | ? | ! |
| Klaus | ! | ? | ? | ? |
| Dorothea | ? | ? | ! | ? |
| Maria | ? | ! | ? | ? |
| Karl - Theodor | ? | ? | ? | ! |
| Hans | ? | ? | ? | ! |
Der einzige, der sich über das Ergebnis aus Stuttgart freute, war der schöne Anton. Es hielt sich nämlich hartnäckig das Gerücht, dass der Anton zwar recht nett anzusehen sei, andererseits aber struntzdumm und vom Gebrauch der Anabolika, naja sie wissen schon ... . Für Schätzerle wurde allerdings klar: Der Mörder war wieder der Gärtner.
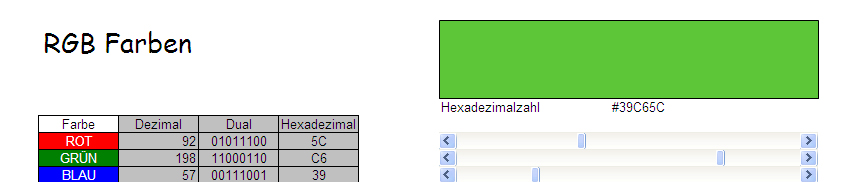
Du hast den Farbfilm vergessen ...
Wir wollen davon ausgehen, dass Sie diesen Text an einem Computermonitor  lesen. Ferner möge es sich bei
lesen. Ferner möge es sich bei  um einen Monitor handeln, der
um einen Monitor handeln, der
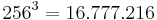
verschiedene Farben darstellen kann. Weil Bilder, für deren Darstellung auf dem Bildschirm 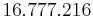 verschiedene Farben zur Verfügung stehen, recht natürlich auf das menschliche Auge wirken, bezeichnet man die Farbtiefe von
verschiedene Farben zur Verfügung stehen, recht natürlich auf das menschliche Auge wirken, bezeichnet man die Farbtiefe von 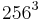 Farben auch als True Color.
Da das Display von
Farben auch als True Color.
Da das Display von  selbst leuchtet, erfolgt die Farbdarstellung auf ihm entsprechend des Prinzips der additiven Farbmischung: Die Farbe eines jeden Pixels wird durch das Mischen der drei Grundfarben Rot, Grün und Blau generiert (RGB).
Für jede der drei Farben stehen jeweils 256 verschiedene Farbtiefen zur Verfügung, d.h. im Farbraum von
selbst leuchtet, erfolgt die Farbdarstellung auf ihm entsprechend des Prinzips der additiven Farbmischung: Die Farbe eines jeden Pixels wird durch das Mischen der drei Grundfarben Rot, Grün und Blau generiert (RGB).
Für jede der drei Farben stehen jeweils 256 verschiedene Farbtiefen zur Verfügung, d.h. im Farbraum von  gibt es 256 verschiedene Rottöne, 256 verschiedene Grüntöne und schließlich 256 verschiedene Blautöne. Jeder der Farbtöne wird durch eine natürliche Zahl
gibt es 256 verschiedene Rottöne, 256 verschiedene Grüntöne und schließlich 256 verschiedene Blautöne. Jeder der Farbtöne wird durch eine natürliche Zahl  mit
mit 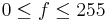 codiert. Der Code einer beliebigen Farbe des Farbraumes von
codiert. Der Code einer beliebigen Farbe des Farbraumes von  ist damit ein geordnetes Tripel
ist damit ein geordnetes Tripel 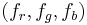 , wobei
, wobei 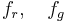 und
und 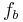 jeweils natürliche Zahlen zwischen
jeweils natürliche Zahlen zwischen 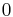 und
und 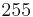 sind und die jeweilige Farbtiefe der Grundfarben Rot, Grün und Blau codieren.
Das folgende Bild ist ein Screenshot einer Excelapplikation [1] zur Verdeutlichung des Prinzips der Generierung von RGB-Farben. Zur Zeit des Screenshots war
sind und die jeweilige Farbtiefe der Grundfarben Rot, Grün und Blau codieren.
Das folgende Bild ist ein Screenshot einer Excelapplikation [1] zur Verdeutlichung des Prinzips der Generierung von RGB-Farben. Zur Zeit des Screenshots war 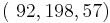 das geordnete Tripel, welches der Füllfarbe des Rechtecks zuzuordnen ist.
das geordnete Tripel, welches der Füllfarbe des Rechtecks zuzuordnen ist.
Aus der abstrakten Sicht des Mathematikers ist unser RGB-Farbraum das Kreuzprodukt 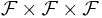 , wobei unter
, wobei unter 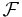 die Menge der natürlichen Zahlen von 0 bis 255 zu verstehen ist.
die Menge der natürlichen Zahlen von 0 bis 255 zu verstehen ist.
Nun möge es sich zugetragen haben, dass wir des Auftrages zur Generierung eines computergestützten Videos anheischig wurden. Als Auftraggeber zeichnet niemand geringeres als Nina Hagen zuständig. Zum 55. Geburtstag der Punk-Diva soll Du hast den Farbfilm vergessen (mein Michael) als Video fröhliche Urständ feiern.
Was liegt bei dem Titel Du hast den Farbfilm vergessen näher, als ein Video in Schwarz/Weiß oder genauer ausgedrückt ein Video , das nur Grautöne verwendet. Der RGB-Farbraum enthält auch Grautöne. Diesbezüglich definieren wir uns eine dreistellige Relation mit dem Namen 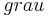 auf der Menge aller geordneten Tripel aus
auf der Menge aller geordneten Tripel aus 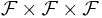 : Die Komponenten
: Die Komponenten 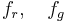 und
und 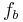 eines Tripels
eines Tripels 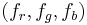 mögen genau dann in der Relation
mögen genau dann in der Relation 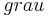 zueinander stehen, wenn das Tripel
zueinander stehen, wenn das Tripel 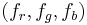 der Code für einen Grauwert ist.
der Code für einen Grauwert ist.
Es wäre interessant zu untersuchen, welche Tripel aus 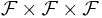 so beschaffen sind, dass ihre jeweiligen Komponenten in der Relation
so beschaffen sind, dass ihre jeweiligen Komponenten in der Relation  zueinander stehen. Bei dieser Formulierung bricht man sich fast die Zunge. Formulieren wir doch einfacher: Wir wollen untersuchen, welche geordneten Tripel aus
zueinander stehen. Bei dieser Formulierung bricht man sich fast die Zunge. Formulieren wir doch einfacher: Wir wollen untersuchen, welche geordneten Tripel aus 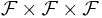 zur Relation
zur Relation 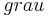 gehören.
gehören.
Für diese Untersuchung stellen wir uns ausnahmsweise ganz dumm und gehen mittels einer Brutal Force- Methode vor:
Beginnend mit dem Tripel 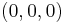 danach die Tripel
danach die Tripel 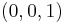 und
und 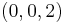 testend probieren wir systematisch alle
testend probieren wir systematisch alle 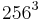 Tripel bis zum Tripel
Tripel bis zum Tripel 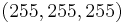 aus, ob sie der Code für einen Grauwert sind oder nicht, bzw. zu unserer Relation
aus, ob sie der Code für einen Grauwert sind oder nicht, bzw. zu unserer Relation 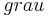 gehören oder nicht. Aus allen potentiell möglichen Tripeln haben wir die Tripel herausgesucht, die zu unserer Relation
gehören oder nicht. Aus allen potentiell möglichen Tripeln haben wir die Tripel herausgesucht, die zu unserer Relation 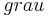 gehören. Anders ausgedrückt: Auf der Suche nach allen geordneten Tripeln, die einen Grauwert codieren, haben wir eine Teilmenge unserer Grundmenge
gehören. Anders ausgedrückt: Auf der Suche nach allen geordneten Tripeln, die einen Grauwert codieren, haben wir eine Teilmenge unserer Grundmenge 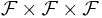 gebildet. Diese Teilmenge ist letztlich unsere Relation.
gebildet. Diese Teilmenge ist letztlich unsere Relation.
Die Untersuchungen ergaben (Der Leser überzeuge sich mittels [2].), dass immer dann ein Grauwert codiert wird, wenn die Komponenten des geordneten Tripels 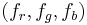 identisch sind:
identisch sind: 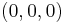 ,
, 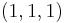 , ...,
, ..., 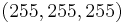 . Unsere Relation
. Unsere Relation 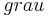 ist damit eine Teilmenge aus
ist damit eine Teilmenge aus 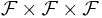 , die 256 geordnete Tripel enthält.
, die 256 geordnete Tripel enthält.
Als Quintessenz unserer Überlegungen können wir unser Relation 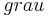 wie folgt präzisieren:
wie folgt präzisieren:
- Definition: (
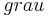 )
)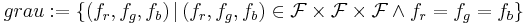
oder - Definition: (
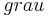 )
)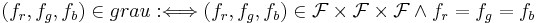
Alles verstanden?
Hier ein kleines Quiz zur Überprüfung Ihres Verständnisses für den Abschnitt mit dem Farbfilm.
Wir legen den folgenden Überlegungen ein kartesisches 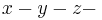 Koordinatensystem zugrunde. Jedem Farbwert
Koordinatensystem zugrunde. Jedem Farbwert 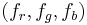 wird genau ein Punkt
wird genau ein Punkt  des
des 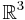 zugeordnet, wobei die
zugeordnet, wobei die 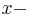 Koordinate von
Koordinate von  dem Rotwert
dem Rotwert 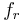 , die
, die 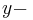 Koordinate von
Koordinate von  dem Grünwert
dem Grünwert 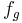 und die
und die 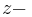 Koordinate von
Koordinate von  dem Blauwert
dem Blauwert 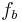 entsprechen.[3] Wir wollen die Menge dieser Punkte als RGB-Farbraum bezeichnen. Alle die Punkte, die einem Grauwert entsprechen, sollen im folgenden die Grauwerte genannt werden.
entsprechen.[3] Wir wollen die Menge dieser Punkte als RGB-Farbraum bezeichnen. Alle die Punkte, die einem Grauwert entsprechen, sollen im folgenden die Grauwerte genannt werden.
Definition des Begriffs der Relation
Definition: (n-stellige Relation)
- Es seien
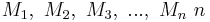 Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus
Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 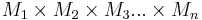 ist eine
ist eine 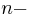 stellige Relation.
stellige Relation.
- Es seien