Diskussion:Lösung von Aufgabe 2.1 (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 9: | Zeile 9: | ||
*Dass <math>\ A</math> und <math>\ B</math> zu <math>\ m</math> ein und denselben Abstand haben, ist notwendig dafür, dass <math>\ m</math> die Mittelsenkrechte von <math>\overline{AB}</math> ist. Hinreichend ist diese Bedingung nicht, wie obige Applikation zeigt. | *Dass <math>\ A</math> und <math>\ B</math> zu <math>\ m</math> ein und denselben Abstand haben, ist notwendig dafür, dass <math>\ m</math> die Mittelsenkrechte von <math>\overline{AB}</math> ist. Hinreichend ist diese Bedingung nicht, wie obige Applikation zeigt. | ||
*Durch die Zusatzbedingung <math>m \perp \overline{AB}</math> könen <math>\ m</math> und <math>\overline{AB}</math> nur noch die folgende Lage zueinander haben:<br /> | *Durch die Zusatzbedingung <math>m \perp \overline{AB}</math> könen <math>\ m</math> und <math>\overline{AB}</math> nur noch die folgende Lage zueinander haben:<br /> | ||
| − | [Bild:Mittelsenkrechte.png|200px] | + | [[Bild:Mittelsenkrechte.png|200px]] |
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 26. April 2011, 15:20 Uhr
Diskussion zu:
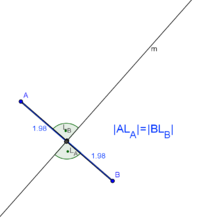
Wenn eine Gerade g zu dem Anfangspunkt und Endpunkt einer Strecke AB ein und denselben Abstand hat und senkrecht auf ihr steht und die Strecke AB schneidet, dann spricht man von der Mittelsenkrechten der Strecke AB.--Celebino 09:35, 20. Apr. 2011 (CEST)
- Unter dem Abstand eines Punktes zu einer Geraden versteht man die Länge des Lotes von dem Punkt auf die Gerade. Natürlich ist der Abstand der Geraden zu dem Punkt dann ebenfalls die Länge des Lotes vom Punkt auf die Gerade. Man spricht aber eher von dem Absatnd eines Punktes zu einer Geraden, als von dem Abstand der Geraden zu einem Punkt. Ihre diesbezügliche Formulierung ist nicht falsch aber etwas unüblich.
- Wenn der Abstand des Punktes
zur Geraden 
gleich dem Abstand des Punktes 
zur Geraden ist, dann könte das noch wie folgt aussehen:
- Dass und zu ein und denselben Abstand haben, ist notwendig dafür, dass die Mittelsenkrechte von
ist. Hinreichend ist diese Bedingung nicht, wie obige Applikation zeigt.
- Durch die Zusatzbedingung
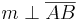könen und nur noch die folgende Lage zueinander haben:
