Lösung von Aufgabe 6.2 (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br /> <math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> [[Category:Einf…“)
 
Zeile 1: Zeile 1:
 
Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br />
 
Untersuchen Sie folgende Relation ''S'' auf ihre Eigenschaften:<br />
−
<math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br />
+
<math>\ g S h \Leftrightarrow \ <math>g \cap h \neq \lbrace \rbrace </math>
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]
 +
 +
 +
 +
Reflexivität: Ja, denn eine Gerade g hat mit sich selbst keine leere Schnittmenge 
 +
<math> g \cap g \neq \lbrace \rbrace </math>
 +
 +
Symmetrie: Ja, denn wenn  h und g keine leere Schnittmenge haben, dann auch g und ha nicht.
 +
Wenn  <math> h \cap g \neq \lbrace \rbrace </math> dann gilt auch  <math> g \cap h \neq \lbrace \rbrace </math>
 +
 +
Transitivität: Nein, denn Wenn g und i keine leere Schittmenge haben und h und i keine Leere Schittmenge haben, dann könten g und h zwei parallele Geraden sein und i eine Gerade die die beiden schneidet. Dann hätten g und h auch keine leere Schittmenge.
 +
Wenn <math>  h \cap i \neq \lbrace \rbrace </math> und <math> g \cap i \neq \lbrace \rbrace </math> dann gilt nicht <math> g \cap h \neq \lbrace \rbrace </math>
 +
 +
--[[Benutzer:Madita|Madita]] 15:15, 19. Mai 2011 (CEST)

Version vom 19. Mai 2011, 14:15 Uhr

Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
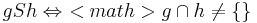
\ g S h \Leftrightarrow \ <math>g \cap h \neq \lbrace \rbrace


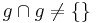
Reflexivität: Ja, denn eine Gerade g hat mit sich selbst keine leere Schnittmenge g \cap g \neq \lbrace \rbrace

Symmetrie: Ja, denn wenn h und g keine leere Schnittmenge haben, dann auch g und ha nicht. Wenn 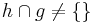h \cap g \neq \lbrace \rbrace dann gilt auch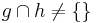 g \cap h \neq \lbrace \rbrace

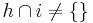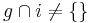Transitivität: Nein, denn Wenn g und i keine leere Schittmenge haben und h und i keine Leere Schittmenge haben, dann könten g und h zwei parallele Geraden sein und i eine Gerade die die beiden schneidet. Dann hätten g und h auch keine leere Schittmenge. Wenn h \cap i \neq \lbrace \rbrace und g \cap i \neq \lbrace \rbrace dann gilt nicht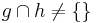 g \cap h \neq \lbrace \rbrace

--Madita 15:15, 19. Mai 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_6.2_(SoSe_11)&oldid=7328“