Lösung von Aufg. 11.4 (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 15: | Zeile 15: | ||
da<math> \overline{AC} \cap g =\lbrace \rbrace \Rightarrow \forall P\epsilon \overline{AC}: P\not\in g</math><br> | da<math> \overline{AC} \cap g =\lbrace \rbrace \Rightarrow \forall P\epsilon \overline{AC}: P\not\in g</math><br> | ||
<math>\Rightarrow \forall P\in \overline{AB} : P \not\in g\Rightarrow Widerspruch</math> zu <math>\overline{AB} \cap g \neq \lbrace \rbrace</math><br\> | <math>\Rightarrow \forall P\in \overline{AB} : P \not\in g\Rightarrow Widerspruch</math> zu <math>\overline{AB} \cap g \neq \lbrace \rbrace</math><br\> | ||
| − | <math>\Rightarrow</math> <math>\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace </math> <br />--[[Benutzer:Peterpummel|Peterpummel]] 16:13, 22. Jun. 2011 (CEST) | + | <math>\Rightarrow</math> <math>\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace </math> <br />--[[Benutzer:Peterpummel|Peterpummel]] 16:13, 22. Jun. 2011 (CEST)<br\> |
| + | |||
| + | Ich bezweifle, dass man hier einfach Zw(A,B,C) voraussetzen darf. [[Benutzer:Mathegott|Mathegott]] 20:30, 23. Jun. 2011 (CEST) | ||
Version vom 23. Juni 2011, 19:30 Uhr
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
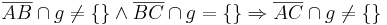
Beweis: durch Widerspruch:
o.B.d.A. gelte 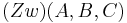
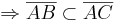
Voraussetztung: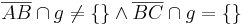
Annahme: 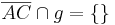
da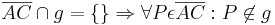
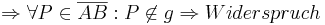 zu
zu 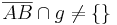

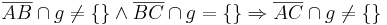
--Peterpummel 16:13, 22. Jun. 2011 (CEST)
Ich bezweifle, dass man hier einfach Zw(A,B,C) voraussetzen darf. Mathegott 20:30, 23. Jun. 2011 (CEST)

