Lösung von Aufg. 11.4 (SoSe 11)
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
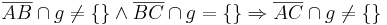
Beweis: durch Widerspruch:
o.B.d.A. gelte 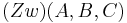
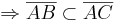
Voraussetztung: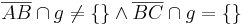
Annahme: 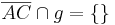
da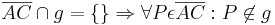
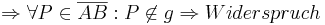 zu
zu 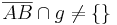

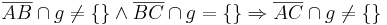
--Peterpummel 16:13, 22. Jun. 2011 (CEST)
Ich bezweifle, dass man hier einfach Zw(A,B,C) voraussetzen darf. Mathegott 20:30, 23. Jun. 2011 (CEST)
Das sehe ich auch so. Besser ist es in Fälle zu unterscheiden. Falls die Fälle dann sehr ähnlich sind, kann man immer noch "Beweis ist analog zu Fall 1." schreiben.
Kann man den Beweis auch direkt führen?--Tutorin Anne 10:53, 24. Jun. 2011 (CEST)
Fallunterscheidung:
1. zw(A,B,C) siehe oben
2. zw (B,A,C) -> Strecke BC schneidet g nicht (Vorraussetzung) -> dann kann g auch nicht die Strecke AB schneiden -> Widerspruch zur Vorraussetzung!
3. zw (A,C,B) -> Strecke AB schneidet g, Strecke CB schneidet g nicht -> Dann muss g die Strecke AC schneiden
--Madita 15:06, 24. Jun. 2011 (CEST)
Anmerkung
Berechtigter Einwand Madita, oBdA ist hier nicht richtig, da die Fälle sich unterscheiden. Danke für die Berichtigung. L.G.--Peterpummel 18:16, 24. Jun. 2011 (CEST)
In der Übung am Montag haben wir diese Aufgabe mit Hilfe des Axiom von Pasch gelöst. Der Beweis war ziemlich komplex. Jetzt stellt sich mir aber die Frage, wieso wir es nicht so lösen dürfen, wie wir es oben gemacht haben? Mathegott 19:54, 28. Jun. 2011 (CEST) Mhhh, ich weiß es nicht. --Tutorin Anne 21:40, 29. Jun. 2011 (CEST)
Beweis mit dem Axiom von Pasch
Aufgrund einer Bitte aus einer Übung werde ich hier den Beweis bereitstellen.
Voraussetzung: 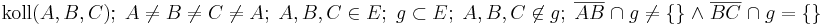
Behauptung: 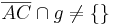
| Beweisschritt | Begründung |
(1) 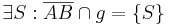 |
Voraussetzung |
(2) 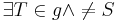 |
Axiom I/2 |
(3) 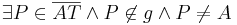 |
Axiom vom Lineal |
(4) 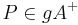 |
(2), (3) |
(5) 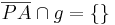 |
(4), Def. Halbebene |
(6) 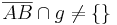 |
Voraussetzung |
(7) 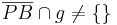 |
(5), (6), Axiom von Pasch |
(8) 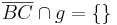 |
Voraussetzung |
(9) 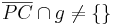 |
(7), (8), Axiom von Pasch |
(10) 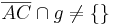 |
(5), (9), Axiom von Pasch |
--Tutor Andreas 17:14, 4. Jul. 2011 (CEST)

