Lösung von Aufg. 11.1 (SoSe 11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 17: Zeile 17:
 
c) <math>\operatorname B</math> Diese Antwort müsste wohl noch ergänzt werden.--[[Benutzer:Andreas|Tutor Andreas]] 11:39, 23. Jun. 2011 (CEST) <br />
 
c) <math>\operatorname B</math> Diese Antwort müsste wohl noch ergänzt werden.--[[Benutzer:Andreas|Tutor Andreas]] 11:39, 23. Jun. 2011 (CEST) <br />
 
B und P <math>\in</math> AB: |PA| = |AB| [[Benutzer:Mathegott|Mathegott]] 20:11, 23. Jun. 2011 (CEST) <br />
 
B und P <math>\in</math> AB: |PA| = |AB| [[Benutzer:Mathegott|Mathegott]] 20:11, 23. Jun. 2011 (CEST) <br />
 +
<br /><br />
 +
Bemerkung: So war es wohl nicht gemeint. Mengen werden in geschweiften Klammern angegeben.--[[Benutzer:*m.g.*|*m.g.*]] 17:47, 26. Jun. 2011 (CEST)
 
d)<math>\operatorname AB</math><br\>--[[Benutzer:Peterpummel|Peterpummel]] 14:39, 22. Jun. 2011 (CEST)
 
d)<math>\operatorname AB</math><br\>--[[Benutzer:Peterpummel|Peterpummel]] 14:39, 22. Jun. 2011 (CEST)

Version vom 26. Juni 2011, 16:47 Uhr

Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?

a) 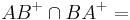\ AB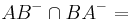^{+} \c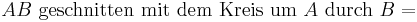ap BA^{+} =

b) \ AB^{-} \cap BA^{-} =

c) \ AB \mathrm{~geschnitten~mit~d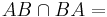em~Kreis~um} \ A \mathrm{~durch} \ B =

d)\ AB \cap BA =

Lösungen:
a) \overline{AB}
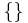
b) \operatorname \lbrace \rbrace
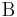c) \operatorname B Diese Antwort müsste wohl noch ergänzt werden.--Tutor Andreas 11:39, 23. Jun. 2011 (CEST)
B und P \in AB: |PA| = |AB| Mathegott 20:11, 23. Jun. 2011 (CEST)


Bemerkung: So war es wohl nicht gemeint. Mengen werden in geschweiften Klammern angegeben.--*m.g.* 17:47, 26. Jun. 2011 (CEST) d)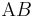\operatorname AB
--Peterpummel 14:39, 22. Jun. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._11.1_(SoSe_11)&oldid=7857“