Lösung von Aufgabe 6.5 (SoSe 11): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
|||
| Zeile 20: | Zeile 20: | ||
<iframe src="http://www.ph-heidelberg.de/wp/gieding/Uebungen/serie%2006/Student%20Submissions_111.png" width="720" height="540" frameborder="2"></iframe><br /><br /><br /><br /> | <iframe src="http://www.ph-heidelberg.de/wp/gieding/Uebungen/serie%2006/Student%20Submissions_111.png" width="720" height="540" frameborder="2"></iframe><br /><br /><br /><br /> | ||
--[[Benutzer:*m.g.*|*m.g.*]] 16:32, 20. Mai 2011 (CEST) | --[[Benutzer:*m.g.*|*m.g.*]] 16:32, 20. Mai 2011 (CEST) | ||
| + | |||
| + | Es handelt sich hierbei um die Relation "befinden sich in ein und derselben Halbebene". | ||
| + | 1) reflexiv, da ein Punkt sich nur in einer Halbebene befinden kann. | ||
| + | 2) symmetrisch: wenn Strecke AB sich in einer Halbebene befinden dann auch Strecke BA (aufgrund der Identität) | ||
| + | 3) transitiv: Wenn Strecke AB und BC sich in der selben Halbebene befinden, dann auch die Strecke AC (Beweisbar mit Axiom von Pasch) [[Benutzer:Mathegott|Mathegott]] 22:03, 15. Jul. 2011 (CEST) | ||
Aktuelle Version vom 15. Juli 2011, 21:03 Uhr
Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation  (
( ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge
ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge 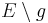 (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige
(also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige 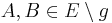 gilt:
gilt: 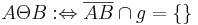 .
.
a) Beschreiben Sie die Relation  verbal und veranschaulichen Sie diese Relation.
verbal und veranschaulichen Sie diese Relation.
b) Begründen Sie anschaulich, dass  eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation
eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation  bezogen.
bezogen.
Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.
a) Die Relation  besagt, dass dann die Strecke AB parallel zur Gerade g ist. Denn nur dann hat die Strecke AB mit g eine leere Schnittmenge. Das heißt, der Abstand A zu g ist gleich groß wie der Abstand von B zu g.
besagt, dass dann die Strecke AB parallel zur Gerade g ist. Denn nur dann hat die Strecke AB mit g eine leere Schnittmenge. Das heißt, der Abstand A zu g ist gleich groß wie der Abstand von B zu g.
b)  ist eine Äquivalenzrelation denn:
ist eine Äquivalenzrelation denn:
Reflexivität: Ein Punkt A hat zur gerade g den gleichen Abstand wie ein Punkt A Symmetrie: Hat A und B zu g den gleichen Abstand, dann auch B und A zu g. Transitivität: Wenn A und B zu g den gleichen Abstand haben und B und C zu g den gleichen Abstand haben, dann auch A zu C. Denn A,B,C müssen alle auf einer Gerade liegen, die parallel zu g liegt.
--Madita 15:24, 19. Mai 2011 (CEST)
Aus der Übung vom 20.05.11:
Stimmt nicht ganz:
[ www.ph-heidelberg.de is not an authorized iframe site ]
--*m.g.* 16:32, 20. Mai 2011 (CEST)
Es handelt sich hierbei um die Relation "befinden sich in ein und derselben Halbebene". 1) reflexiv, da ein Punkt sich nur in einer Halbebene befinden kann. 2) symmetrisch: wenn Strecke AB sich in einer Halbebene befinden dann auch Strecke BA (aufgrund der Identität) 3) transitiv: Wenn Strecke AB und BC sich in der selben Halbebene befinden, dann auch die Strecke AC (Beweisbar mit Axiom von Pasch) Mathegott 22:03, 15. Jul. 2011 (CEST)

