Tangentenkriterium: Unterschied zwischen den Versionen
(→Satz 1: (Tangete am Kreis)) |
(→Satz 2: (Tangente am Kreis)) |
||
| Zeile 57: | Zeile 57: | ||
<ggb_applet width="1366" height="604" version="3.2" ggbBase64="UEsDBBQACAAIALdV+D4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VhNb+M2ED13fwXBQ29x9GE7NmploaaXAJumgNM99FJQ0thmI1Fakkpk//oOScmW7SR1ki2aBggkzoyGM+/NjCjPPjdFTh5AKl6KiPoDjxIQaZlxsYxorRdnE/r58tNsCeUSEsnIopQF0xENBwE18ppffvphplblI2G5NfnK4TGiC5YroERVElimVgB6T87qhuecyfVt8hekWu0Uzsm1qGrcRcsaZWmRfeGqW57bDauc61/4A89AkrxMIzoeYeh49xWk5inLIzr0nCSIaHCgRFFotKtS8k0ptDHfOc9ZAjkCMNfrHAh5MNrQqRZoTIjiG0CwAiObnVsMZlCnOc84EyZPGyIaEfLIM71C23A8xu2AL1eYx9gLnLu0LGU2XysNBWn+AFlGdDSZGBLWbhUGF2alMGbcceRZVX9l3cDDHLTGiBVhDezAXEqe7S2u1c9lvhNVJRf6ilW6lpbvsBXZxCOKe0kTcCyWObSyAOlYQXqflM3coRA613fryj5iA0qWV2VeSiIN9CM0aK+Ju1obE+nWyrM2nrVofRinW70/DayFvSbu6rjiwoXWZu53Wftetw1XxAgMjFim2+QtyxGlpBZcf+kWWB73baq+e+DXukiwP/oFsvXpfy+fs/OD+pndgxSQuyIRyG1d1sqVotvLBpJBygtcOkULCTN0/Y4BOGkGSwld4K67HGBW6/UL8UA8O++CMDEojDXVOCYwH21yMV2ssYPMXca0kZg+yKEAbBJt68HQs4VF033G9AqBEaCULSvdLyA7UEo7G7op0DnZsoDqZ+oHp0i1YnjXNUjO1jgn+glbb7eLhQJNmohOTF9F9GzY096U2T5ITCDYFgFs2Mq4N3RWAFk7ObsUSIUb2o7qcWUhVmYz18XtM5t+mKdAA9+Es1GupKDBWZhy3ZaRg99SVhRMZESwAq1+M31t8edmtBLmRXQdYx23WNa6k944R+3jR4zaAbFl44a+hS0/cDPBXtuZcCpn/zorQcuK3wXiRqKZ5rs3QR/ol/CJ//SPEdofFv9c0B8CnrPwoGpPxme/EK+4THM4qMQbzM93aB2WY/pyOeJg4ukWy/R7TJhe+u8fMUd8nNbjfAniAUMrpSKk8VrU115bpptO0iBqZ65y/Y4av8cNUi95Q+LOPu6sYjwCnY0H3t4fhhGH7RbxsPMcj/AuGDwzfrCUUr7g6cusXwuN7ztM6ID41BGPDcOCXtg9/uPXjKP4TeNoPLTUmkviLm8lt9cuwWA4nA4n04thcDEJffy33eO9r3tOwzF4Asf5a3Ccfxgcj2CcuBf1O3Gcw9LInxlDR+AlL4OnWm8dPMnHH0N9hNuzz1MViwgPB5MpClEzGo3H4ejiHWcVXuzOKhbg3LxxtkWNb6njM+49QGU+Lm7FnWRCmQ9QZ9M7O7+F5fkRy9nrWM7+jyw/1U8bc/A9ZHn0kWnGM6/ESMyppsXxDhqNBxtURPTHb3Wpf8JvfZWuOCQYOtZDuiLmqx6XYuAMrNN9ijV6ofsu/0v6lGZS25M7MRyGg8nFtP/X9a23Lx73J2MftvP+Z5z96aL9Wefyb1BLBwgVjlAWlgQAAAgSAABQSwECFAAUAAgACAC3Vfg+FY5QFpYEAAAIEgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAANAEAAAAAA==" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="1366" height="604" version="3.2" ggbBase64="UEsDBBQACAAIALdV+D4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VhNb+M2ED13fwXBQ29x9GE7NmploaaXAJumgNM99FJQ0thmI1Fakkpk//oOScmW7SR1ki2aBggkzoyGM+/NjCjPPjdFTh5AKl6KiPoDjxIQaZlxsYxorRdnE/r58tNsCeUSEsnIopQF0xENBwE18ppffvphplblI2G5NfnK4TGiC5YroERVElimVgB6T87qhuecyfVt8hekWu0Uzsm1qGrcRcsaZWmRfeGqW57bDauc61/4A89AkrxMIzoeYeh49xWk5inLIzr0nCSIaHCgRFFotKtS8k0ptDHfOc9ZAjkCMNfrHAh5MNrQqRZoTIjiG0CwAiObnVsMZlCnOc84EyZPGyIaEfLIM71C23A8xu2AL1eYx9gLnLu0LGU2XysNBWn+AFlGdDSZGBLWbhUGF2alMGbcceRZVX9l3cDDHLTGiBVhDezAXEqe7S2u1c9lvhNVJRf6ilW6lpbvsBXZxCOKe0kTcCyWObSyAOlYQXqflM3coRA613fryj5iA0qWV2VeSiIN9CM0aK+Ju1obE+nWyrM2nrVofRinW70/DayFvSbu6rjiwoXWZu53Wftetw1XxAgMjFim2+QtyxGlpBZcf+kWWB73baq+e+DXukiwP/oFsvXpfy+fs/OD+pndgxSQuyIRyG1d1sqVotvLBpJBygtcOkULCTN0/Y4BOGkGSwld4K67HGBW6/UL8UA8O++CMDEojDXVOCYwH21yMV2ssYPMXca0kZg+yKEAbBJt68HQs4VF033G9AqBEaCULSvdLyA7UEo7G7op0DnZsoDqZ+oHp0i1YnjXNUjO1jgn+glbb7eLhQJNmohOTF9F9GzY096U2T5ITCDYFgFs2Mq4N3RWAFk7ObsUSIUb2o7qcWUhVmYz18XtM5t+mKdAA9+Es1GupKDBWZhy3ZaRg99SVhRMZESwAq1+M31t8edmtBLmRXQdYx23WNa6k944R+3jR4zaAbFl44a+hS0/cDPBXtuZcCpn/zorQcuK3wXiRqKZ5rs3QR/ol/CJ//SPEdofFv9c0B8CnrPwoGpPxme/EK+4THM4qMQbzM93aB2WY/pyOeJg4ukWy/R7TJhe+u8fMUd8nNbjfAniAUMrpSKk8VrU115bpptO0iBqZ65y/Y4av8cNUi95Q+LOPu6sYjwCnY0H3t4fhhGH7RbxsPMcj/AuGDwzfrCUUr7g6cusXwuN7ztM6ID41BGPDcOCXtg9/uPXjKP4TeNoPLTUmkviLm8lt9cuwWA4nA4n04thcDEJffy33eO9r3tOwzF4Asf5a3Ccfxgcj2CcuBf1O3Gcw9LInxlDR+AlL4OnWm8dPMnHH0N9hNuzz1MViwgPB5MpClEzGo3H4ejiHWcVXuzOKhbg3LxxtkWNb6njM+49QGU+Lm7FnWRCmQ9QZ9M7O7+F5fkRy9nrWM7+jyw/1U8bc/A9ZHn0kWnGM6/ESMyppsXxDhqNBxtURPTHb3Wpf8JvfZWuOCQYOtZDuiLmqx6XYuAMrNN9ijV6ofsu/0v6lGZS25M7MRyGg8nFtP/X9a23Lx73J2MftvP+Z5z96aL9Wefyb1BLBwgVjlAWlgQAAAgSAABQSwECFAAUAAgACAC3Vfg+FY5QFpYEAAAIEgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAANAEAAAAAA==" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
<br />--[[Benutzer:HecklF|Flo60]] 10:53, 24. Jul. 2011 (CEST) | <br />--[[Benutzer:HecklF|Flo60]] 10:53, 24. Jul. 2011 (CEST) | ||
| + | Gut! Aber auch hier lieber ein paar Schritte mehr!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:34, 24. Jul. 2011 (CEST) | ||
Version vom 24. Juli 2011, 15:34 Uhr
Inhaltsverzeichnis |
Tangentenkriterium
Kriterium: (Tangete am Kreis)
- Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.
- Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.
Satz 1: (Tangete am Kreis)
Beweis durch Wiederspruch:
Voraussetzung: 
Behauptung: 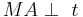
Annahme: 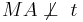
| 1 | Es existiert ein Lot von M auf t, dieses ist eindeutig. Der Lotfußpunkt auf k heiße B. | Ex. und Eindeutigkeit Lot, Annahme, Voraussetzung |
| 2 | CB| = |BA| | Axiom vom Lineal, Abstandsaxiom, Definition zwischenrelation, Voraussetzung, (1) und Skizze |
| 3 | 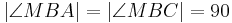 |
nach Konstruktion, Def. NW, Def. supplementär, Supplementaxiom, Def. Lot (1) |
| 4 | 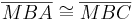 |
SWS, (2), (3) und weil trivialerweise  zu sich selbst kongruent ist. zu sich selbst kongruent ist.
|
| 5 | MC| = |MA| = r nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist. |
--Flo60 10:53, 24. Jul. 2011 (CEST)
Beweisidee und Begründung ist richtig. Schöner wäre der Beweis sicher, wenn du mehrer kleinen Schritte aufführst, anstatt mit 6 Begründungen einen riesen Schritt durchführst.--Tutorin Anne 16:31, 24. Jul. 2011 (CEST)
Satz 2: (Tangente am Kreis)
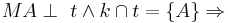 t ist Tangente an k.
t ist Tangente an k.
Eigentlich erscheint dieser Beweis komisch. Allerdings könnte es ja sein, dass wenn eine Gerade durch eben einen Punkt A verläuft und senkrecht auf dem Berührradius steht, dass dann trotzdem ein zweiter Schnittpunkt vorhanden ist mit k und dann wäre halt t keine Tangente mehr.
Voraussetzung: 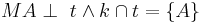
Behauptung: t ist Tangente an k
Annahme: Es ex. ein Punkt S: 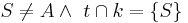
Ich versuche diesen Beweis bewusst in der absoluten Geometrie zu Beweisen. Mit der Innenwinklesumme wäre es natürlich noch einfacher, aber zwecks der Übung.
| 1 |  |
Annahme, Definiton Kreis und Radius |
| 2 | 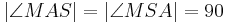 |
Voraussetzung, Basiswinkelsatz, (1), Def. Senkrecht |
| 3 | Demnach sind im Dreieck zwei Winkel nicht spitz, was ein Widerspruch zu einem der Korollare ist. Demnach ist die Annahme zu verwerfen. | Korollar des schwachen Außenwinkelsatzes, (2), Definition Dreieck |
--Flo60 10:53, 24. Jul. 2011 (CEST)
Gut! Aber auch hier lieber ein paar Schritte mehr!--Tutorin Anne 16:34, 24. Jul. 2011 (CEST)