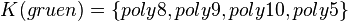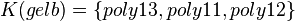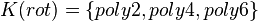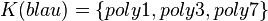Zusammenhang zwischen Äquivalenzrelationen und Klasseneinteilungen WS 11/12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Gegeben sei die Menge der nachstehend dargestellten Vielecke.<br /> <ggb_applet width="800" height="400" version="3.2" ggbBase64="UEsDBBQACAAIADNdbj0AAAAAAAAAAAA…“) |
RicRic (Diskussion | Beiträge) |
||
| Zeile 4: | Zeile 4: | ||
'''Aufgabe:''' Teilen Sie die Menge aller dargestellten Vielecke in Klassen ein, indem Sie eine Relation formulieren, so dass alle Elemente einer Klasse in dieser Relation zueinander stehen, und dass beliebige Elemente zweier verschiedener Klassen nicht in dieser Relation zueinander stehen.<br /> | '''Aufgabe:''' Teilen Sie die Menge aller dargestellten Vielecke in Klassen ein, indem Sie eine Relation formulieren, so dass alle Elemente einer Klasse in dieser Relation zueinander stehen, und dass beliebige Elemente zweier verschiedener Klassen nicht in dieser Relation zueinander stehen.<br /> | ||
| − | * | + | * <math>K(gruen)=\left\{ {poly8,poly9,poly10,poly5} \right\}</math> |
| − | * | + | * <math>K(gelb)=\left\{ {poly13,poly11,poly12} \right\}</math> |
| − | * | + | * <math>K(rot)=\left\{ {poly2,poly4,poly6} \right\}</math> |
| + | * <math>K(blau)=\left\{ {poly1,poly3,poly7} \right\}</math> | ||
Welche Eigenschaften hat ihre Relation?<br /> | Welche Eigenschaften hat ihre Relation?<br /> | ||
| − | + | * gleiche Farbe | |
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 5. November 2011, 18:28 Uhr
Gegeben sei die Menge der nachstehend dargestellten Vielecke.
Aufgabe: Teilen Sie die Menge aller dargestellten Vielecke in Klassen ein, indem Sie eine Relation formulieren, so dass alle Elemente einer Klasse in dieser Relation zueinander stehen, und dass beliebige Elemente zweier verschiedener Klassen nicht in dieser Relation zueinander stehen.
Welche Eigenschaften hat ihre Relation?
- gleiche Farbe